АМСОИ (10) - Лекция №3 - Анализ характеристик функционирования СМО

Этот конспект ещё не дописан. Здесь не хватает:    - графиков и некоторых расчётов для этого примера

Анализ разомкнутых СМО с обратной связью

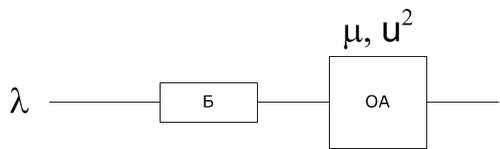
Анализ характеристик функционирования СМО М/М/1

$P(t) = 1 - e^{-\frac{t}{t_0} }$ - вероятность того или иного времени обслуживания и времени пребывания.

$t_0 = \frac{1}{\mu}$

$T = \frac{t_0}{1 - \rho}$

Пример

$\lambda = 10$ заявок/сек.

Найти такую $\mu$, чтобы с вероятностью $P = 0.95$ среднее время предывания было меньше 1 секунды.

$\rho = \frac{\lambda}{\mu} = \frac{10}{\mu}$

$P(T_{0.095}) < 1$

Среднее время: $T < \frac{1}{3} = 0.333$ секунды.

$0.333 = \frac{1}{\mu\cdot (1 - \frac{10\mu})} = \frac{\mu}{\mu\cdot (\mu - 10)} = \frac{1}{\mu - 10}$

$0.333\cdot (\mu - 10) = 1$

$\mu\geq\frac{4.33}{0.333} = 13$ заявок/сек.

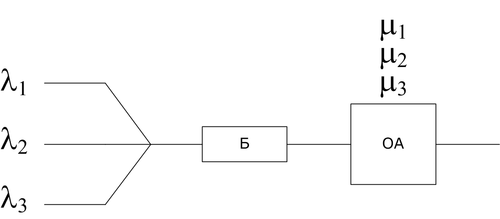
Анализ характеристик функционирования СМО Мn/Мn/1

Mn - означает, что у каждого входного потока свои функции распределения (разные типы заявок).

При анализе СМО данного типа находится среднее число заявок в системе и среднее время ожидания, которое является общим и одинаковым для всех типов заявок.

Пример

Найти характеристики функционирования СМО.

Ищем общую загрузку СМО:

$\rho = \sum_{i = 1}^n\frac{\lambda_i}{\mu_i} < 1$

Находим среднее время обслуживания заявок разных типов:

$t_0 = \sum_{i = 1}^n \frac{\lambda_i}{\lambda}\cdot t_i$

Определяем второй момент времени обслуживания:

$t_0^{(2)} = \sum_{i = 1}^n \frac{\lambda_i}{\lambda}\cdot t_i^{(2)}$

Далее находим среднее время ожидания (будет общим для всех):

$W = \frac{\lambda\cdot t_0^{(2)} }{2\cdot (1 - \rho)}$

Дальше таблица:

№ потока	$\lambda_i$	$\mu_i$	$t_i = \frac{1}{\mu_i}$	$\nu^2 = \frac{1}{К_эрл}$	$t^{(2)}$	$\rho_i = \frac{\lambda_i}{\mu_i}$
$\lambda_1$, детерминированный ($К_{эрл} = \infty$)	0.5	2	0.5	0	0.25	0.25
$\lambda_2$, пуассоновский	0.1	0.5	2	1	8	0.2
$\lambda_3$, эрландовский ($К_{эрл} = 5$)	0.03	0.2	5	0.2	30	0.15

Суммарная загрузка $\rho = 0.25 + 0.2 + 0.15 = 0.6 < 1$

$\lambda = \sum_{i = 1}^n\lambda_i = 0.63$ заявок в секунду.

$t_0 = \sum_{i = 1}^n\frac{\lambda_i}{\lambda}\cdot t_i = 0.94$ секунд.

$t_0^{(2)} = \sum_{i = 1}^n \frac{\lambda_i}{\lambda}\cdot t_i^{(2)} = 2.89$ секунд.

$W = \frac{\lambda\cdot t_0^{(2)} }{2\cdot (1 - \rho)} = 2.28$ секунд.

Анализ характеристик функционирования СМО с эрланговскими потоками

М/Ек/1 - обслуживание у такой СМО эрланговское.

$\nu^2 = \frac{1}{К_{эрл} }$

Используется формула Поллячека-Хинчина, она касается среднего количества заявок в очереди: $Q = \frac{\rho^2\cdot (1 + \nu_0^2)}{2\cdot (1 - \rho)}$

$\nu_0^2 = \frac{1}{К_{эрл} } = \frac{1}{2} = 0.5$

$\nu_0^2 = 0$

$L = Q + \rho = Q + \frac{\lambda}{\mu}$

$W = \frac{Q}{\lambda}$

$T = \frac{L}{\lambda}$

Tr/Ек/1 - у такой СМО ещё и поток заявок эрланговский.

Для неё есть формула Файнберга: $Q = \frac{\rho^2\cdot (\nu_{вх}^2 + \nu_0^2)}{2\cdot (1 - \rho)}$

Пример сравнения экспоненциального и регулярного

Определить, насколько улучшатся характеристики функционирования СМО при переходе от экспоненциального обслуживания к регулярному при загрузке $\rho = 0.8$?

Ищем и сравниваем:

Характеристика	Экспоненциальное обслуживание	Регулярное обслуживание
$Q$	3.2	1.6
$L$	4	2.4
$W$	$\frac{3.2}{\lambda}$	$\frac{1.6}{\lambda}$
$T$	$\frac{4}{\lambda}$	$\frac{2.4}{\lambda}$