АМСОИ (10) - Лекция №10 - Анализ замкнутых СМО методом Базена
Вся задача из лекции должна быть в тетрадях с домашним заданием, так как она типа как бы является домашним заданием №7.
Нужно найти погрешность для $$T_ц$$ между методом Базена и методом узкого места.
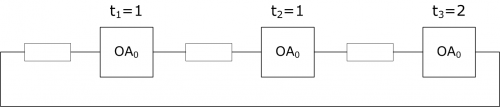
$$$N = 4$$$
Шаги:
1) определение коэффициентов Базена
$$$x_1 = 1$$$
$$$x_i = \frac{t_i}{t_1}\cdot P_i$$$
где:
- $$P_i$$ - вероятность обращения к фазе.
2) строим матрицу Базена
$$$g(m,n) = g(n,m-1) + x_i\cdot g\cdot (n-1,m)$$$
где:
- $$m$$ - по горизонтали
- $$n$$ - по вертикали
| $$x_1$$ | $$x_2$$ | $$x_3$$ | |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 1 | 2 | 4 |
| 2 | 1 | 3 | 11 |
| 3 | 1 | 4 | 26 |
| 4 | 1 | 5 | 57 |
3) определяем коэффициент использования (загрузку):
$$$U_1 = \frac{G(N-1)}{G(N)} = \frac{26}{57}$$$
$$$U_2 = U_1\cdot x_2 = \frac{26}{57}$$$
$$$U_3 = U_2\cdot x_3 = \frac{26}{57}\cdot 2 = \frac{52}{57}$$$
4) определяем количество заявок в каждой СМО в буфере и на обслуживании:
$$$L_1 = \sum_{i=1}^n\frac{G(n-i)}{G(n)} = \frac{26 + 11 + 4 + 1}{57} = \frac{42}{57}$$$
$$$L_2 = \sum_{i=1}^n\frac{x_2^i\cdot G(n-i)}{G(n)} = 1\cdot\frac{42}{57}$$$
$$$L_3 = \sum_{i=1}^n\frac{x_3^i\cdot G(n-i)}{G(n)} = \frac{2\cdot 26 + 2^2\cdot 11 + 2^3\cdot 4 + 2^4\cdot 1}{57} = \frac{144}{57}$$$
Проверка на количество заявок:
$$$\sum_{i=1}^3 L_i = \frac{42}{57} + \frac{42}{57} + \frac{144}{57} = \frac{228}{57} = 4 = N$$$
5) находим время пребывания:
$$$T_ц = \frac{N\cdot t_1}{U_1} = \frac{228}{26} = 8.77$$$
$$$\lambda = \frac{N}{T_ц} = \frac{104}{228}$$$
$$$T_i = \frac{L_i}{\lambda}$$$
$$$T_1 = \frac{21}{13}$$$
$$$T_2 = \frac{21}{13}$$$
$$$T_3 = \frac{144}{26}$$$
Теперь эту же задачу методом узкого места:
$$$T_ц = N\cdot t_{max} + \sum_{i=1}^k \frac{t_i}{t_{max} }\cdot t_i = 9$$$
$$$T_ц = 4\cdot 2 + 0.5\cdot 1 + 0.5\cdot 1 = 9$$$
А теперь погрешность между методом Базена и узким местом:
$$$\delta= \frac{9 - 8.77}{8.77} = 8\%$$$