АМСОИ (10) - Лекция №1 - СМО

Системы и сети массового обслуживания

Массовое обслуживание

СМО

Системы массового обслуживания.

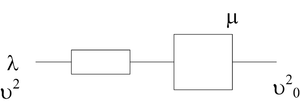
Здесь:

• $\lambda$ - интенсивность входного потока заявок;
• $\nu$ - интенсивность обслуживания. Отношение дисперсии к квадрату матожидания;
• $\nu^2_0$ - квадрат коэффициента вариаций. Отношение среднего квадратического отклонения к матожиданию;
• $\mu$ - очередь.

Обозначения:

• $a$ - тип входного потока:
  • $M$ - пуассоновский поток;
• $b$ - тип обслуживания;
  • $M$ - экспоненциальное;
• $c$ - количество аппаратов;
  • $1$ - один обслуживающий аппарат;
• $d$ - ёмкость очереди;
  • $\infty$ - очередь бесконечна;
• $e$ - дисциплина выбора заявок из очереди на обслуживание;
  • $FIFO$ - FIFO;
• $f$ - количество источников заявок;
  • $\infty$ - бесконечный поток.

Существует Эрландовский входной поток: $К_{эрл} = \frac{1}{\nu^2}$

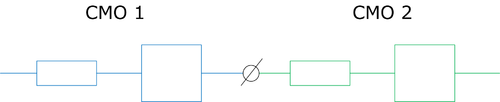
СеМО

Сеть массового обслуживания.

Параметры:

• $\rho = \frac{\lambda}{\mu} < 1$ - загрузка системы;
• $Q$ - количество заявок в очереди;
• $L = Q + \rho$ - количество заявок в системе;
• $W$ - время ожидания (время нахождения в очереди);
• $T = W + \frac{1}{\mu} = W + t_0$ - время нахождения в системе.

Расчёт загрузки:

	СМО M/M/1	СМО M/M/2
$\rho$	$\frac{\lambda}{\mu}$	$\frac{\lambda}{2\cdot\mu}$
$Q$	$\frac{\rho^2}{1 - \rho}$	$\frac{2\cdot\rho^3}{1 - \rho^2}$
$L$	$\frac{\rho}{1 - \rho}$	$\frac{2\cdot\rho}{1 - \rho^2}$
$W$	$\frac{\rho\cdot t_0}{1 - \rho}$	$\frac{\rho^2\cdot t_0}{1 - \rho^2}$
$T$	$\frac{t_0}{1 - \rho}$	$\frac{t_0}{1 - \rho^2}$

$Q = \lambda\cdot W$

$L = \lambda\cdot T$

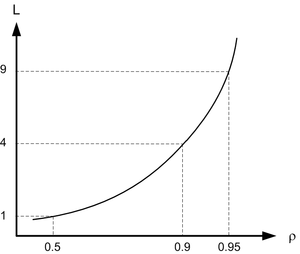
Зависимость примерно такая:

Дальше что-то происходит:

$\frac{Q_2}{Q_1} = \frac{2\cdot\rho^3\cdot (1 - \rho)}{(1 - \rho^2)\cdot \rho^2} = \frac{2\cdot\rho}{1 + \rho}$

$\frac{L_2}{L_1} = \frac{2\cdot\rho\cdot (1 - \rho)}{(1 - \rho^2)\cdot \rho} = \frac{2}{1 + \rho}$

$\frac{T_2}{T_1} = \frac{t_{02}\cdot\ (1 - \rho)}{(1 - \rho^2)\cdot t_{02} } = \frac{\mu_1}{\mu_2\cdot (1 + \rho)} = \frac{2}{1 + \rho}$

Один обслуживающий аппарат более эффективен, чем два, равных в сумме ему по производительности. Поэтому выбирая между одним, обрабатывающим 10 заявок в час, и двумя, в сумме оба тоже обрабатывающими 10 в час, надо выбирать его.

Домашнее задание №1

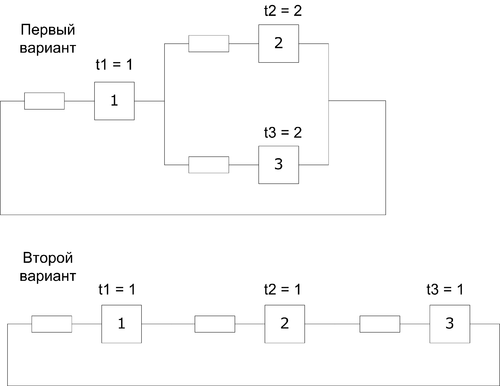
Выбрать, какая система обслуживания в магазине будет лучше.

Одновременно в системе (магазине) может находиться 3, 6 или 10 покупателей.

Промоделировать можно на модели из курсового прошлого семестра: рабочие станции с нулевым временем. Для первого варианта схемы канал с временем 0.01, а остальное - сервер и диски. Для второго варианта: канал, сервер, диск.