АМСОИ (10) - Лекция №2 - Методика разработки формализованных схем
Задача для примера
Имеется мастерская по обслуживанию серверов.
Поток клиентов составляет $$\lambda$$ клиентов/час.
Убыток от клиентов в очереди составляет $$S = 15$$ долларов/клиентов в час
Есть возможность нанять сотрудников $$C_1$$ или $$C_2$$.
$$C_1$$ обслуживает $$\mu_1 = 3$$ клиента в час, требует денег $$S_1 = 6$$ долларов/час.
$$C_2$$ обслуживает $$\mu_2 = 4$$ клиента в час, требует денег $$S_2 = 10$$ долларов/час.
Задача руководителя: оптимизировать работу мастерской.
Считается, что поток клиентов подчиняется закону Пуассона, а обслуживание клиентов - экспоненциальному.
Для оценки эффективности работы фирмы следует использовать следующие выражение, показывающие убытки фирмы:
$$S_{\sum} = n_i\cdot S_i + S\cdot Q$$ $$S$$ - зарплата; $$n$$ - количество сотрудников $$i$$-го типа; $$S\cdot Q$$ - убытки от пребывания клиентов в очереди.
Если работают сотрудники $$C_1$$ или сотрудники $$C_2$$, то их работу можно описать в виде работы многоканальной СМО: количество ОА равно количеству сотрудников, а производительность равна работе сотрубников.
Рассмотрим пять вариантов работы:
| Исходные данные | Вариант 1 $$C_1$$ |
Вариант 2 $$C_1 + C_1$$ |
Вариант 3 $$C_1 + C_1 + C_1$$ |
Вариант 4 $$C_2$$ |
Вариант 5 $$C_2 + C_2$$ |
|---|---|---|---|---|---|
| Загрузка аппарата, $$\rho = \frac{\lambda}{\mu\cdot C}$$, где $$С$$ - количество ОА | $$\rho_1 = 0.667$$ | $$\rho_1 = 0.333$$ | $$\rho_1 = 0.222$$ | $$\rho_1 = 0.5$$ | $$\rho_1 = 0.25$$ |
| Тип СМО | M/M/1 | M/M/2 | M/M/3 | M/M/1 | M/M/2 |
| Количество заявок в очереди, $$Q = \frac{C\cdot\rho^{C+1} }{1 - \rho^C}$$ | 1.333 | 0.082 | 0.0075 | 0.5 | 0.033 |
| Сумарные потери фирмы, $$S_{\sum}$$ | 26 | 13.25 | 18.1 | 17.5 | 20.5 |
| Ранжирование вариантов по предпочтительности | 5 | 1 | 3 | 2 | 4 |
Вот и выбрали лучший вариант.
Методика разработки формализованных схем
Включает пять этапов:
- разработка структурной схемы исследуемой СОИ. Схема включает, как правило, коммутаторы, маршрутизаторы, сервера и рабочие станции и прочее оборудование. Количество запросов в системе равно количеству рабочих станций - они их генерируют, потому на них очередей нет, а есть очереди на канале и сервере;
- выделение основных компонентов СОИ и схемы их взаимодействия;
- представление компонентов СОИ в виде СМО;
- разработка формализованных схем СМО;
- разработка формализованной схемы исследуемой СОИ.
Если сервер многоядерный или многопроцессорный, то его можно представить в виде многоканального ОА.
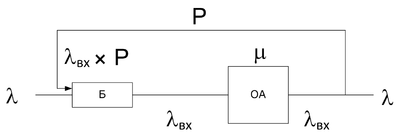
Анализ разомкнутых СМО с обратной связью
$$P$$ - вероятность повторного поступления заявки на обслуживание.
$$\lambda = \lambda + \lambda_{вх}\cdot P$$
$$\lambda = \lambda_{вх}\cdot (1 - P)$$
$$\alpha = \frac{1}{1-P}$$ - среднее количество проходов заявки через ОА за время пребывания этой заявки в СМО.
$$\lambda_{вх} = \frac{\lambda}{1 - P} = \alpha\cdot\lambda$$
Основные формулы для расчёта рассматриваемой системы:
- загрузка ОА: $$\rho = \frac{\lambda_{вх} }{\mu} = \frac{\alpha\cdot\lambda}{\mu} = \alpha\cdot\frac{\lambda}{\mu}$$;
- количество заявок в очереди: $$Q = \frac{\rho^2}{1 - \rho}$$;
- количество заявок в системе: $$L = Q + \rho = \frac{\rho}{1 - \rho}$$;
- определяем времена:
- $$W = \frac{Q}{\lambda_{вх} }$$;
- $$T = \frac{L}{\lambda_{вх} }$$.
$$W_{\sum} = \alpha\cdot W$$
$$T_{\sum} = \alpha\cdot T$$
Если в процессе анализа окажется, что $$\rho = \alpha\cdot\frac{\lambda}{\mu}\ge 1$$, то значит где-то ошибка, потому что может быть только $$\rho < 1$$. Тогда надо уменьшать вероятность, или повышать производительность, или ставить дополнительные ОА.
Пример
Исходные данные:
- $$\lambda = 4$$;
- $$\mu = 10$$;
- $$P = 0.5$$.
$$\alpha = \frac{1}{1 - P} = 2$$
$$\rho = 2\cdot\frac{4}{10} = 0.8$$
$$Q = \frac{0.8^2}{0.2} = 3.2$$
$$L = \frac{0.8}{0.2} = 4$$
$$W_{\sum} = \frac{3.2}{4} = 0.8$$
$$T_{\sum} = \frac{4}{4} = 1$$
Домашнее задание №2
Сравнительный анализ времени пребывания заявок в одноканальной и двухканальной СМО.
Построить график зависимости по трём значениям загруженности: 0.1, 0.5 и 0.9.
M/M/1 - $$T_1$$.
M/M/2 - $$T_2$$.
$$\Delta T = \frac{T_2 - T_1}{T_1}$$
$$\mu_1 = 2\cdot\mu_2$$.
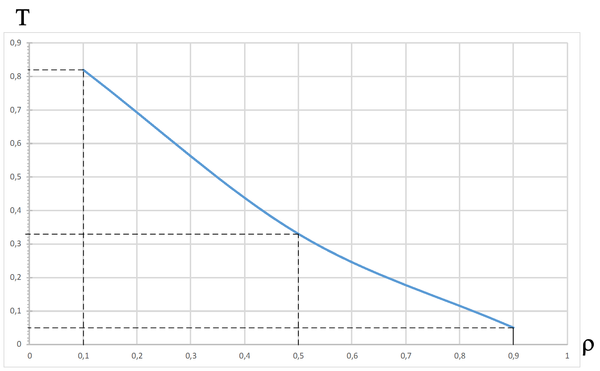
Ищем $$\Delta T$$:
- $$\Delta T_{\rho_1} = 0.82$$
- $$\Delta T_{\rho_2} = 0.33$$
- $$\Delta T_{\rho_3} = 0.05$$
График: