АМСОИ (10) - Лекция №5 - Анализ СМО с ограниченной очередью

Этот конспект ещё не дописан. Здесь не хватает:    - всех примеров

Анализ СМО с ограниченной длиной очереди

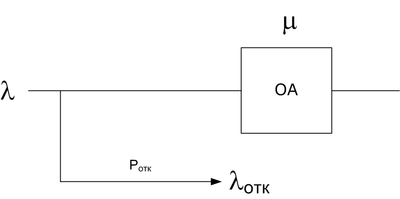
M/M/1/0

Вероятность отказа - вероятность того, что заявка, поступающая в систему, застаёт ОА занятым, а очередь полностью заполнена.

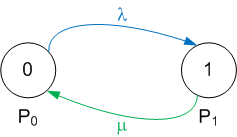
Тут два состояния:

$P_{отк} + P_{обслуж} = 1$

$\sum_{i = 0}^n P_{i} = 1$

где:

n - число возможных состояний системы

$\nu^2_{сист} = \nu_{вх}\cdot P_i + (1 - P_i) = P_i + 1 - P_i = 0$

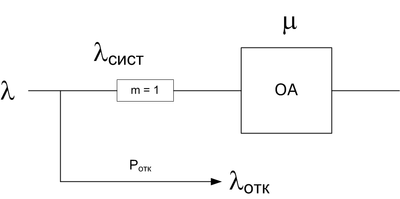
Буфер с с ёмкостью 1

Рассмотрим буфер с ёмкостью 1:

Теперь стало 3 состояния:

$P_0\cdot\lambda = P_1\cdot\mu$

$P_1\cdot (\lambda + \mu) = P_0\cdot\lambda + P_2\cdot\mu$

$P_2\cdot\mu = P_1\cdot\lambda$

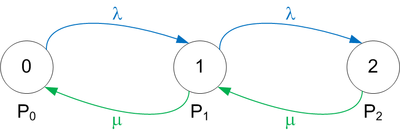
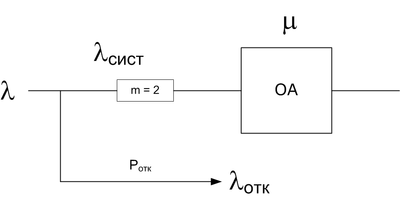
Буфер с с ёмкостью 2

Рассмотрим буфер с ёмкостью 2:

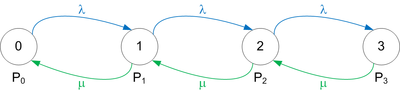
Теперь стало 4 состояния:

Для частного случая, когда все вероятности равны и $\lambda = \mu$:

$P_{отк} = P_3 = \frac{1}{4}$

$\lambda_{отк} = P_{отк}\cdot\lambda = \frac{1}{4}\cdot\lambda$

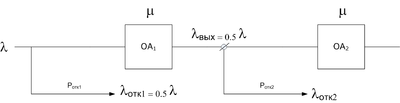
Две СМО

Теперь рассмотрим две СМО:

$P_0\cdot\lambda_{вх2} = P_1\cdot\mu$

$P_0\cdot\lambda_{вых1} = P_1\cdot\mu$

$P_0\cdot\frac{1}{2}\lambda_{вх2} = P_1\cdot\mu$

Тут какие-то расчёты и короче: до выхода второго ОА будет добираться только треть начального количества заявок, поступающих на вход всей системы ($\frac{1}{3}\cdot\lambda$).