АМСОИ (10) - Лекция №7 - Анализ разомкнутых СеМО

Разомкнутые сети массового обслуживания

Порядок анализа:

1. разбить исходную СМО на несколько;
2. составить систему уравнений, в которой для каждой СМО присутствует своё уравнение;
3. решить систему и определить реальных входные потоки для каждой СМО: $\lambda_i = \alpha_i\cdot \lambda$, где $\alpha_i$ - сколько раз входной поток проходит через $i$-ой СМО за время пребывания;
4. определить загрузку каждой СМО: $\rho_i = \frac{\lambda_i}{\mu_i\cdot c_i} = \frac{\alpha_i\cdot\lambda}{\mu_i\cdot c_i}$, где $c_i$ - количество ОА в $i$-ой СМО;
5. представляем каждую СМО в виде СМО типа M/M/C;
6. определить характеристики функционирования.

Тип M/M/C:

• пуассоновский входной поток;
• экспоненциальное обслуживание;
• C - количество ОА;
• ёмкость входного буфера бесконечна;
• FIFO;
• ёмкость генератора заявок бесконечна.

Характеристики функционирования:

$T = \sum_{i=1}^n T_i$;

$W = \sum_{i=1}^n W_i$;

$L = \sum_{i=1}^n L_i$;

$Q = \sum_{i=1}^n Q_i$.

Пример разомкнутой СеМО

Каждая СМО является M/M/1.

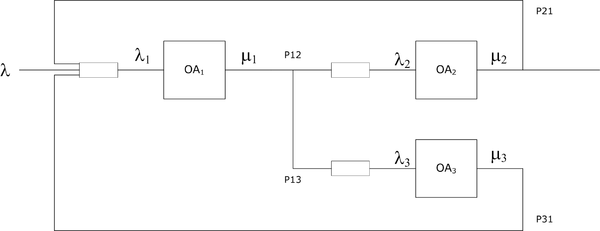
Исходные данные:

$\lambda = 1$

$\mu_1 = 10$, $\mu_2 = 8$, $\mu_3 = 5$

$P_{12} = 0.75$, $P_{13} = 0.25$, $P_{21} = 0.5$, $P_{31} = 1$

Система уравнений:

$\lambda_1 = \lambda + \lambda_2\cdot P_{21} + \lambda_3$

$\lambda_2 = \lambda_1\cdot P_{12}$

$\lambda_3 = \lambda_1\cdot P_{13}$

Заменяем и считаем:

$\alpha_1\cdot\lambda = \lambda + \alpha_2\cdot\lambda\cdot P_{21} + \lambda_3 = 2.67$

$\alpha_2\cdot\lambda = \alpha_1\cdot\lambda\cdot P_{12} = 2$

$\alpha_3\cdot\lambda = \alpha_1\lambda\cdot P_{13} = 0.67$

Загрузка:

$\rho_1 = \frac{2.67\cdot 1}{10\cdot 1} = 0.267$

$\rho_2 = \frac{2\cdot 1}{8\cdot 1} = 0.25$

$\rho_3 = \frac{0.67\cdot 1}{5\cdot 1} = 0.134$

Характеристики:

$Q_i = \frac{\rho_i^2}{1 - \rho_i}$

$L_i = Q_i + \rho_i = \frac{\rho_i}{1 - \rho_i}$

$W_i = \alpha_i\cdot\frac{Q_i}{\lambda_i}$

$T_i = \alpha_i\cdot\frac{L_i}{\lambda_i}$

Параметр	СМО1	СМО2	СМО3	СеМО
$\rho$	0.267	0.25	0.134	-
$Q$	0.097	0.083	0.021	0.201
$L$	0.364	0.333	0.155	0.852
$W$	0.097	0.083	0.021	0.201
$T$	0.364	0.333	0.155	0.852

Ещё пример разомкнутой СеМО

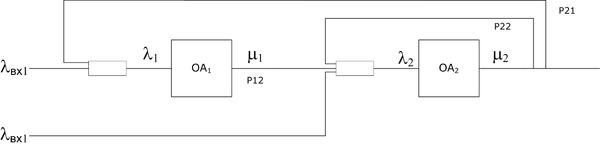
Исходные данные:

$\lambda_{вх1} = 1$, $\mu_1 = 8$

$\lambda_{вх2} = 2$, $\mu_2 = 10$

$P_{12} = 1$, $P_{21} = 0.4$, $P_{22} = 0.2$

Система уравнений:

$\lambda_1 = \lambda_{вх1} + \lambda_2\cdot P_{21}$

$\lambda_2 = \lambda_{вх1} + \lambda_2\cdot P_{22} +\lambda_1$

Из входных потоков выбираем минимальный. Все остальные имеют коэффициент относительно $\lambda$, то есть у нас это $2\cdot\lambda$

Заменяем:

$\alpha_1\cdot\lambda = \lambda + \alpha_2\cdot\lambda\cdot P_{21}$

$\alpha_2\cdot\lambda = \alpha_2\cdot\lambda\cdot P_{22}$

Считаем:

$\alpha_1 = 2.67$, $\lambda_1 = 4$, $\rho_1 = 0.5$

$\alpha_2 = 2$, $\lambda_2 = 7.5$, $\rho_2 = 0.75$

Характеристики посчитать дома:

Параметр	СМО1	СМО2	СМО3	СеМО
$\rho$	0	0	0	-
$Q$	0	0	0	0
$L$	0	0	0	0
$W$	0	0	0	0
$T$	0	0	0	0

Домашнее задание №5

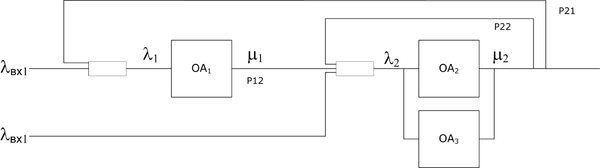
Исходные данные:

$\lambda_{вх1} = 1$, $\mu_1 = 8$

$\lambda_{вх2} = 2$, $\mu_2 = 10$

$P_{12} = 1$, $P_{21} = 0.4$, $P_{22} = 0.2$