АМСОИ (10) - Лекция №8 - Приоритетное обслуживание в СМО

Этот конспект ещё не дописан. Здесь не хватает:    - домашнего задания    - ещё адских формул и вычислений

Приоритетное обслуживание заявок в СМО

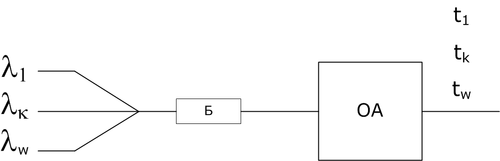
Если обслуживание приоритетное, и все заявки выстраиваются в одну очередь, то среднее время ожидания:

$$W = \frac{\sum_{k=1}^n\rho_k\cdot t_k\cdot (1 + \nu_k^2)}{2\cdot (1 - \rho)}$$

Экспоненциальное обслуживание $k$-го потока:

$$\nu_k^2 = 1$$

$$\rho = \sum_{k=1}^n\rho_k$$

Например, имеется 2 потока заявок:

$\lambda_1 = 0.3$, $\mu_1 = 1$

$\lambda_2 = 0.25$, $\mu_2 = 0.5$

Заявки обслуживаются в порядке поступления, приоритетов нет, обслуживание экспоненциальное.

$$t = \frac{1}{\mu}$$

$$W = \frac{\rho_1\cdot t_1 + \rho_2\cdot t_2}{1 - \rho} = \frac{0.3\cdot 1 + 0.5\cdot 2}{1 - 0.8} = 6.5$$

Пояснения:

M/M/1:

$\rho = \frac{\lambda}{\mu}$

$Q = \frac{\rho^2}{1 - \rho}$

$L = Q + \rho = \frac{\rho}{1 - \rho}$

$W = \frac{Q}{\lambda} = \frac{\rho^2}{(1 - \rho)\cdot\rho\mu} = \frac{\rho}{(1 - \rho)\cdot\mu} = \frac{\rho\cdot t}{1 - \rho}$

$T = \frac{L}{\lambda} = \frac{\rho}{(1 - \rho)\cdot\mu} = \frac{t}{1 - \rho} = W + \frac{1}{\mu} = W + t$

Относительные приоритеты

$W_k$ - среднее время ожидания в очереди заявки $k$-го приоритета

$$W_k = \frac{\sum_{i=1}^n\rho_i\cdot t_i\cdot (1 + \nu_k^2)}{2\cdot (1 - \sum_{i=1}^{k-1}\rho_i)\cdot (1 - \sum_{i=1}^k\rho_i)}$$ где:

$k - 1$ - количество приоритетов, предшествующих исходному;

$n$ - общее число типов заявок, которые поступают в систему;

$i$ - заявка $i$-го приоритета.

Относительные приоритеты - заявка, поступившая в систему, не прерывается, а обслуживается полностью. После этого в систему поступает заявка с наивысшим приоритетом.

Пример для двух классов приоритетов: выражение упрощается и принимает следующий вид:

$$W = \frac{\rho_1\cdot t_1 + \rho_2\cdot t_2}{1 - \rho_1} = \frac{0.3\cdot 1 + 0.5\cdot 2}{1 - 0.3} = 1.852$$

$$W = \frac{\rho_1\cdot t_1 + \rho_2\cdot t_2}{(1 - \rho_1)\cdot (1 - \rho_1 - \rho_2)} = \frac{0.3\cdot 1 + 0.5\cdot 2}{(1 - 0.3)\cdot (1 - 0.8)} = 9.280$$

Проверка правильности выполненных расчётов осуществляется по закону сохранения Клейрока (слева - относительный приоритет, справа - без приоритета):

$$\rho_1\cdot W_1 + \rho_2\cdot W_2 = \rho\cdot W$$

$$0.3\cdot 1.852 + 0.5\cdot 9.280 = 0.8\cdot 6.5$$

$$5.2 = 5.2$$

Не рекомендуется вводить более 3 приоритетов.

Абсолютные приоритеты

Такие заявки прерывают обслуживание заявок более низкого приоритета.

$$W_k = \frac{\sum_{i=1}^n\rho_i\cdot t_k}{1 - \sum_{i=1}^{k-1}\rho_i} + \frac{\sum_{i=1}^k\rho_i t_i\cdot (1 - \nu_i^2)}{2\cdot (1 - \sum_{i=1}^{k-1}\rho_i)\cdot (1 - \sum_{i=1}^k\rho_i)}$$

$$W_1 = \frac{\rho_1\cdot t_1}{1 - \rho_1} = \frac{0.3\cdot 1}{1 - 0.3} = 0.422$$

$$W_2 = \frac{\rho_1\cdot t_2}{1 - \rho_1} + \frac{\rho_1\cdot t_1 + \rho_2\cdot t_2}{(1 - \rho_1)\cdot (1 - \rho_1 - \rho_2)} = \frac{0.3\cdot 2}{1 - 0.3} + \frac{0.3\cdot 1 + 0.5\cdot 2}{(1 - 0.3)\cdot (1 - 0.8)} = 10.14$$

Домашнее задание №6

Здесь должно быть.