АМСОИ (10) - Лекция №9 - Замкнутые СМО

Этот конспект ещё не дописан. Здесь не хватает:    - примеров

Замкнутые СМО

Модель ремонтника

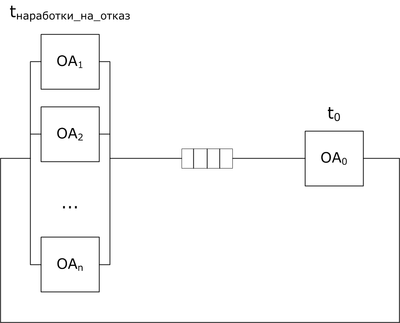
Подход к решению:

1) используя формулу Мальма (или Пальма), определяем вероятность простоя ремонтника:

$$\Psi = \frac{\mu_{НО} }{\mu_0} = \frac{t_0}{t_{НО} }$$

$$P_0 = \Bigl(\sum_{k=0}^N \frac{N!\cdot\Psi^k}{(N - k)!}\Bigr)^{-1}$$

2) испольуя формулу Литтла:

$$T_{цикла} = \frac{N\cdot t_0}{U_0}$$ где:

$U_0 = 1 - P_0$ - коэффицент использования.

3) находим время пребывания в ремонте (в очереди + сам ремонт):

$$T_{ремонта} = T_{цикла} - t_{НО}$$

4) находим количество заявок в ремонте:

$$L = \lambda\cdot T_{ремонта} = \frac{N}{T_{цикла} }\cdot T_{ремонта} = N\cdot\frac{T_{ремонта} }{T_{цикла} }$$

5) количество заявок в очереди:

$$Q = L - U_0$$

6) время нахождения в очереди:

$$W = T_{ремонта} - t_0$$

Метод фонового потока

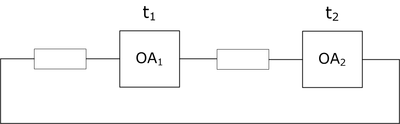
$T_1 = T_2$

$T_{цикла} = T_1 + T_2$

$T_1 = \frac{t}{1 - \rho_{фоновая_1} } = \frac{(N + 1)\cdot t_1}{2}$, $\rho_{фоновая}$ - загрузка обслуживающего аппарата потоком фоновых задач.

$\rho_{фоновая_1} = \lambda_{фоновая_1}\cdot t_1$

$\lambda_{фоновая} = \frac{N - 1}{T_{цикла} }$

$\lambda_{фоновая}$ - поток фоновых задач (которые создаются всеми, кроме рассматриваемой).

Для большего количества фаз:

$$U = \frac{N}{N + 1}$$

$$P_0 = \frac{1}{N + 1}$$

$$U + P_0 = 1$$

$$U_\sum = 2\cdot U = \frac{2\cdot N}{N + 1}$$

Метод узкого места

Для приблизительной оценки общего времени пребывания в последовательном тракте (сколько трафик идёт от отправителя к получателя).

1) определяем узел, у которого наибольшее время обслуживания. Если таких несколько, то выбираем любой из них;

2) определяем время цикла:

приближённая формула:

$$T_{цикла} = N\cdot t_{max} + \sum_{i=1}^{k-1} t_i$$

точная формула:

$$T_{цикла} = N\cdot t_{max} + \sum_{i=1}^{k-1}\frac{t_i}{t_{max} }\cdot t_i$$