НиД (10) - Лекция №12 - Псевдоэлементы (продолжение)
...начало

Метод псевдоэлементов
Математическое обоснование композиции и декомпозиции
В ТМО с редкими событиями эти редкие очереди могут внести серьёзные погрешности.
$$$К_г = \frac{1}{1 + \lambda\cdot m_{t_в} }$$$
$$$К_с = \frac{\lambda}{2}\cdot К_г^2\cdot (D_{t_в} + m_{t_в})$$$
$$$D_{t_в} = \frac{2\cdot К_с}{\lambda\cdot К_г^2} - m_{t_в}^2$$$
Последовательная композиция
Наша аппроксимация:
$$$К_{ГА}(t) = К_г + (1 - К_г)\cdot e^{-\frac{1 - К_г}{К_с}\cdot t}$$$
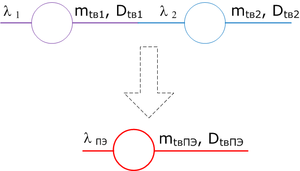
$$$\lambda_{ПЭ} = \lambda_1 + \lambda_2$$$
$$$К_{г_{ПЭ} } = К_{г_1}\cdot К_{г_2}$$$
$$$К_{Г_1}(t) = К_{г_1} + (1 - К_{г_1})\cdot e^{-\frac{1 - К_{г_1} }{К_{с_1} }\cdot t}$$$
$$$К_{Г_2}(t) = К_{г_2} + (1 - К_{г_2})\cdot e^{-\frac{1 - К_{г_2} }{К_{с_2} }\cdot t}$$$
$$$К_{Г_{ПЭ} }(t) = К_{c_{ПЭ} } = \int_0^\infty t\cdot \Bigl[-К_{г_{ПЭ} }'(t)\Bigr] dt$$$
$$$К_{Г_{ПЭ} } = \frac{К_{с_1}^2\cdot К_{г_2}\cdot(1 - К_{г_2}) + К_{c_1}\cdot К_{с_2}\cdot (1 - К_{К_{ПЭ} }) + К_{с_2}^2\cdot К_{г_1}\cdot (1 - К_{г_2})}{К_{с_1}\cdot (1 - К_{г_1}) + К_{с_2}\cdot (1 - К_{г_2})}$$$
Последовательная декомпозиция
Теперь надо наоборот - найти один из скомпозированных через известный псевдоэлемент.
$$$\lambda_2 = \lambda_{ПЭ} - \lambda_1$$$
$$$К_{г_2} = \frac{К_{ПЭ} }{К_{г_1} }$$$
Квадратное уравнение:
$$$A\cdot К_{с_2}^2 + B\cdot К_{с_2} + C = 0$$$
$$$К_{с_2} = \frac{-B + \sqrt{B^2 - 4\cdot A\cdot C} }{2\cdot A}$$$
здесь:
- $$A = К_{г_1}\cdot (1 - К_{г_1})$$
- $$B = К_{с_1}\cdot (1 - К_{г_{ПЭ} }) - К_{с_{ПЭ} }\cdot (1 - К_{г_1})$$
- $$C = К_{с_1}\cdot (К_{с_1}\cdot К_{г_2} - К_{с_{ПЭ} })\cdot (1 - К_{г_2})$$
Параллельная композиция
Если мы находим параметры надёжности параллельно включённой схемы, у которой каждый элемент имеет экспоненциальное распределение времени наработки на отказ, то эквивалентный элемент этой схемы имеет функцию распределения времени наработки на отказ, отличную от экспоненциальной. Однако, это отличие незначительное, и можно аппроксимировать её к экспоненциальной.
Так как потоки отказов элементов пуассоновские, а элементы работают независимо, то поток отказов из двух параллельных элементов будет ординарным.
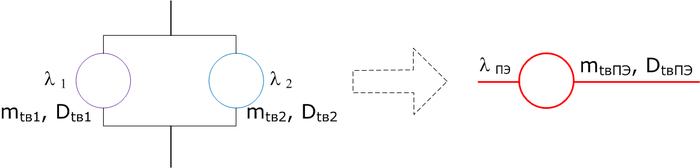
$$$\lambda_{ПЭ} = \frac{К_{г_1}\cdot (1 - К_{г_2})\cdot\lambda_1 + К_{г_2}\cdot (1 - К_{г_1})\lambda_2}{К_{г_1} + К_{г_2} - К_{г_1}\cdot К_{г_2} }$$$
$$$К_c = \int_0^\infty t\cdot \Bigl[- К_{г_{ПЭ} }'(t)\Bigr] dt$$$
$$$К_{с_{ПЭ} } = \frac{К_{с_1}^2\cdot (1 - К_{г_2})^2 + К_{с_1}\cdot К_{с_2}\cdot (1 - К_{г_{ПЭ} }) + К_{с_2}^2\cdot (1 - К_{г_1})^2}{К_{с_1}\cdot (1 - К_{г_2}) + К_{с_2}\cdot (1 - К_{г_1})}$$$
Параллельная декомпозиция
Так же, как и в последовательной, ищем второй элемент через известный псевдоэлемент и первый.
$$$К_{г_2} = \frac{К_{г_{ПЭ} } - К_{г_1} }{1 - К_{г_1} }$$$
$$$\lambda_2 = \frac{К_{г_{ПЭ} }\cdot\lambda_{ПЭ} - К_{г_1}\cdot (1 - К_{г_2})\cdot\lambda_1}{К_{г_2}\cdot (1 - К_{г_1})}$$$
Квадратное уравнение:
$$$A\cdot К_{с_2}^2 + B\cdot К_{с_2} + C = 0$$$
$$$К_{с_2} = \frac{-B + \sqrt{B^2 - 4\cdot A\cdot C} }{2\cdot A}$$$
здесь:
- $$A = (1 - К_{г_1})^2$$
- $$B = К_{с_1}\cdot (1 - К_{г_{ПЭ} }) - К_{с_{ПЭ} }\cdot (1 - К_{г_1})$$
- $$C = К_{с_1}\cdot (1 - К_{г_2})\cdot \Bigl(К_{с_1}\cdot (1 - К_{г_2}) - К_{с_{ПЭ} }\Bigr)$$
Материал будет продолжен через одну лекцию.
продолжение...
Дополнение к ЛР-ДЗ №3
Нужно будет найти наименее надёжные элементы.
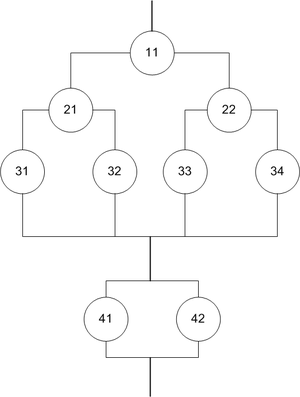
Чтобы проранжировать показатели нажёжности по каждому рангу, надо:
- определить показатели надёжности всей схемы в целом (например, методом певдоэлементов);
- исследуемые элементы какого-либо ранга принимаются абсолютно надёжными (выбрасываются из схемы, остаются только линии) и находятся параметры надёжности оставшейся схемы;
- используя последовательную декомпозицию, найти параметры надёжности этих (исключённых) элементов. Таким образом находятся показатели надёжности для каждого ранга;
- теперь проранжируем их. Сразу станет видно наименее надёжный.
