НиД (10) - Лекция №13 - Время пребывания в группе состояний

Этот конспект ещё не дописан. Здесь не хватает:    - скольких-то формул    - нескольких графов

Материал по работам Овчаров Льва Александровича.

Нахождение функции распределения времени пребывания в группе состояний

Состояния системы $\xi(t)$.

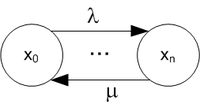
Составляем систему уравнений, всё как всегда. Стационарный режим, производные равны нулю, и $P_0 = \frac{\lambda_0}{\mu_1}\cdot P_1 = \rho_1\cdot P_1$, а $P_1 = \rho_2\cdot P_2$ и так далее.

$$P_0 = \frac{1}{1 + \sum_{k=0}^{n-1}\Pi_{i=0}^k\frac{\lambda_i}{\mu_{i+1} } }$$

И вот ставится задача найти функцию распределения времени пребывания в некоторых состояниях (однократного в них пребывания).

Например, состояния $x_3, x_4, x_5$ являются рабочими - если система находится в них, то она работоспособна, и при отказе система перейдёт в состояние $x_2$ или $x_6$.

Выделим из общего графа часть с этими состояниями. Все переходы будут кодироваться $\lambda_{из состояния, в состояние}$

$$P_{i-1}' = \lambda_{i,i-1}\cdot P_i(t)$$

$$P_{i}' = (\lambda_{i,i+1} + \lambda_{i,i-1})\cdot P_i(t) + \lambda_{i,i+1}\cdot P_{i+1}(t)$$

$$P_{i-1}(0) = 0$$

$$P_{j+1}(0) = 0$$

$$\sum_{k=i}^j P_{k}(0) = 1$$

Для наших условий найдём функцию распределения $F(t)$ времени $T$ пребывания системы в группе состояний ${x_i..x_j}$. Эта функция равна вероятности того, что это время $T$ будет меньше, чем текущее $t$. То есть, это означает, что к моменту времени $t$ система не будет находится в нашей группе состояний (будет неисправна), а будет находиться либо в $x_{i-1}$, либо в $x_{j+1}$.

Значит:

$$F(t) = P_{i-1}(t) + P_{j+1}(t)$$

$$f(t) = \frac{dF(t)}{dt} = \frac{dP_{i-1}(t)}{dt} + \frac{dP_{j+1}(t)}{dt}$$

Хотя наш новый граф отличается от исходного, но закон распределения времени пребывания в группе состояний будет таким же.

Можем теперь найти математическое ожидание:

$$m[t] = \overline{t} = \int_0^\infty t\cdot f(t) dt$$

$$m[T^2] = \alpha = \int_0^\infty t^2\cdot f(t) dt$$

$$D[t] = m[T^2] - (m[t])^2$$

Теперь возьмём наш граф без поглощающих (неисправных) состояний. В результате кучки формул получится:

$$\Pi_{i..n} = \sum_{j=1}^n P_j$$

На основании эргодического свойства это будет равно:

$$\Pi_{i..n} = \frac{\overline{t}_{i..n} }{\overline{t}_{i-1} + \overline{t}_{i..n} }$$

$$\overline{t}_{i-1} = \frac{1}{\lambda_{i-1,i} }$$

$$\overline{t}_{i..n} = \overline{t}_{i-1}\cdot\frac{\Pi_{i..n} }{1 - \Pi_{i..n} }$$

В подавляющем большинстве случаев функция распределения времени нахождения в группе состояний является экспоненциальной, значит:

$$\lambda = \frac{1}{\overline{t}_{i..n} }$$

$$f(t) = \lambda\cdot e^{-\lambda\cdot t}$$

Адаптация для псевдоэлементов и ограниченного восстановления

Рассмотренный выше метод можно использовать для адаптации метода псевдоэлементов для систем с ограниченным восстановлением.

Определим время нахождения в группе состояний:

$$T_0 = \frac{1}{\mu_{n-k+1} }\cdot \frac{\sum_{j=0}^{n-k} P_j}{P_{n-k+1} }...$$

$$P_0 = \frac{1}{1 + \sum{j=1}^{n-k}\Pi_{i=1}^j P_j}$$

$$T_{неогр.} = \frac{(n-k)!\cdot\mu^{n-k} }{\Pi_{i=1}^{n-k+1} \lambda_i}$$

Таким образом, если не учесть ограниченное или неограниченное восстановление, то ошибка будет равна:

$$\frac{T_{неогр.} }{T_{огр.} } = (n-k)!$$

В ряде случаев эта погрешность будет отсутствовать, а в других случаях может быть огромной.

Поэтому было предложено для случаев с ограниченным восстановлением находить некоторое значение $\mu_{экв}$ и считать с ним, как с неограниченным. Для этого $\mu_{экв}$ должно быть таким, чтобы время наработки на отказ у неограниченного и ограниченного были равны.

$$\mu_{экв_i} = \frac{\mu_{экв_{i-1} } }{\Bigl(\frac{T_{НО_{i-1} } }{T}\Bigr)^{\frac{1}{n-k} } }$$

$$\mu_{экв_1} = \Bigl(\frac{\Pi_{i=1}^{n-k+1} \mu_i}{(n - k)!}\Bigr)^{\frac{1}{n-k} }$$