НиД (10) - Лекция №5 - Расчёт восстанавливаемых систем

Показатели надёжности восстанавливаемых систем

Восстановление - какой-либо ремонт: замена, устранение неисправностей.

Самопроизвольное восстановление считается сбоем - не сам факт восстановления, а то, что произошла неисправность и сама же исчезла, и система самовосстановилась.

Восстанавливаемые вне процесса применения

Такие системы можно считать системами с мгновенными восстановлением.

Поток отказов:

Суммарная наработка на отказ до возникновения $n$-го отказа: $T_n = T_1 + T_2 + ... + T_n$

Поток отказов можно описывать:

• ведущей функцией потока отказов $\Omega$ - число отказов на интервале от $0$ до $t$;
• параметром потока отказов - $\omega$ - среднее число отказов в малом интервале времени.

Если потоки событий являются ординарными - когда вероятность появления двух и более одновременных событий бесконечно мала по сравнению с вероятностью появления одного события - то параметр $\Omega$ = $\omega$

Вероятность исправной работы:

$$P(\vartriangle t) = exp(-\int^{t_2}_{t_1}\omega\cdot\vartriangle (t)dt)$$

Всё это верно для систем с ограниченным последействием - вероятность появления отказа на интервале $(t_1, t_2)$ зависит от наработки, накопленной от последнего отказа, и не зависит от того, когда произошли предыдущие отказы.

Для реальных систем:

$$\omega_{службы} = \frac{1}{t_{службы} }\cdot\int_0^{t_р} \omega (t)dt$$

$$\omega = \frac{1}{m_{t_р} } $$

Восстанавливаемые в процессе применения

Системы, в которых недопустимы перерывы в работе, также восстанавливаются в процессе применения. Это возможно благодаря избыточности (наличию резерва), присутствующей в этих системах.

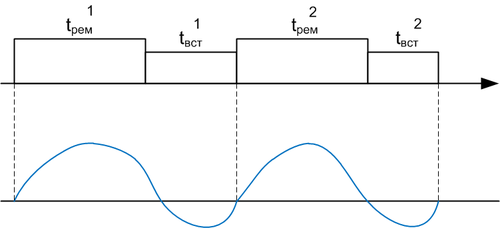
Готовность - способность системы находиться в процессе эксплуатации в работоспособном состоянии и быть готовой к применению.

Функция распределения времени работы: $f(t)$

Функция распределения времени восстановления: $q(t)$

Функция распределения восстановления системы - композиция этих двух потоков:

$$f_0(t) = \int_0^t f(x)\cdot q(t - x)dx$$

Поток восстановления: $\omega_0(t)$

Функция готовности системы: $Г(t)$

Функция простоя (неготовности) системы: $П(t) = 1 - Г(t)$

$$Г(t) = P(t) + \int_0^t P(t - \tau)\cdot\omega_0(\tau)d\tau$$

Коэффициент готовности:

$$Г(t) = \frac{1}{m_{t_р} + m_{t_0} }\cdot\int_0^\infty P(t)dt = \frac{m_{t_р} }{m_{t_р} + m_{t_0} } = К_Г$$

Для восстанавливаемых систем $К_Г$ должен дополняться ещё другими характеристиками (минимум две), потому что коэффициенты для двух случаев, например, могут быть равны, но в первом система 1 час работала и 3 часа восстанавливалась, а вторая 3 часа работала и 1 час восстанавливалась.

$\overline{К_Г} = \frac{1}{t_сл}\int_0^{t_{ср} } Г(t)dt$ - для случая неограниченного восстановления.

$К_Г = \frac{m_{t_р} }{m_{t_р} + m_{t_0} } = \frac{\mu}{\mu + \lambda}$

$Г(t) = \frac{\mu}{\mu + \lambda} + \frac{\lambda}{\mu + \lambda}\cdot exp(-(\mu + \lambda))\cdot t$

$\rho = \frac{\lambda}{\mu}$ - коэффициент загрузки

$К_Г = \frac{1}{1 + \rho}$

При увеличении $\rho$ коэффициент готовности уменьшается, но стационарный режим устанавливается быстрее.

$$Г(t) = \frac{1}{1 + \rho}\cdot (1 + \rho\cdot e^{-\mu\cdot(1 + \rho)\cdot t}) $$

$$Г(t) = К_Г + (1 - К_Г)\cdot e^{-\frac{t}{К_Г\cdot m_{t_в} } } $$

Если $\lambda = const$ и $\mu = const$, то в начальный момент работы системы $Г(t)\approx P(t)$

При маленьких $t$ можно $Г(t)\approx 1 - \frac{t}{m_t}$