СПАСОИ (10) - Лекция №7 - Индексация данных

Этап логического проектирования

Методы индексации данных в реляционных БД

B-индексы

Строятся для следующих атрибутов:

• первичный ключ. Значение атрибутов в индексе уникально;
• альтернативный ключ. Значение атрибутов в индексе уникально;
• инвертированный ключ - произвольный атрибут или набор атрибутов. Значения атрибутов в индексе могут повторяться.

Типы B-индексов:

• обычные индексы - B-tree;
• битовые индексы - Bit Mapped Index;
• реверсивные индексы - Reverse Key Index;
• индекс-таблица - Table Index.

B-tree

Каждая запись блока листового уровня имеет следующий вид:

<
    значение атрибута(ов) - mean,
    идентификатор записи таблицы БД - rowid
>

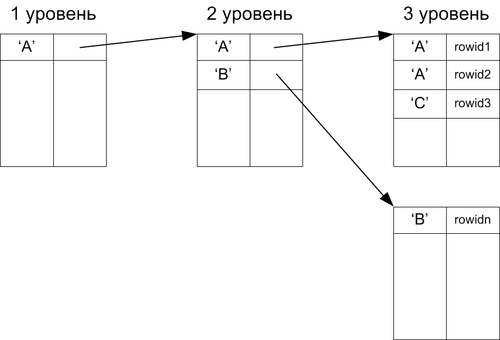
B - то есть бинарным - называется потому, что при переполнении блока индекса (они имеют ограниченный размер) он расщепляется на два примерно равных блока (появляется новый), а в блок предыдущего уровня добавляется указатель на новый.

Индексы строятся для конкретного атрибута(ов) конкретной таблицы.

Предположим, что индекс построен для некоторого атрибута q. Записи блока третьего уровня показывают, что в таблицах хранятся следующие значения:

rowid имеет сложную структуру: AABCDD.AAY.AB7890.056 - 18 байт.

где:

AABCDD - идентификатор объекта;

AAY - относительный идентификатор файла;

AB7890 - блок внутри файла;

056 - запись внутри блока.

Рассмотрим определение числа уровней в B-деревьеях.

Пусть:

$V$ - число записей в таблице БД;

$k$ - максимальное число записей в одном блоке индекса;

$l$ - число уровней индекса.

Тогда:

$\frac{V}{k}$ - число блоков самого низшего, листового уровня;

$\frac{V}{k^2}$ - число блоков $l-1$ уровня;

...

$\frac{V}{k^l} = 1$ - число блоков первого уровня.

Тогда число уровней: $$l = \log_k V$$

Оценим объём индекса на листовом уровне. Будем предполагать, что все блоки на этом уровне заполнены.

Введём следующие обозначения:

$V$ - число записей в таблице БД;

$Lq$ - длина индексируемого атрибута;

$Lr$ - длина указателя на запись.

Получаем числов блоков $$Q = V\cdot (Lq + Lr)$$

Предположим, задана следующая таблица:

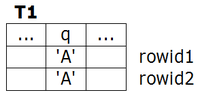
T1

...	q	S
...	'A'	'B'

И выдаётся запрос с условием

SELECT * FROM T1
WHERE q = 'A' AND S = 'B'

Возможны следующие варианты:

1)

1. система определяет идентификаторы записей по условию q = 'A', используя индекс для q.
2. определяется список идентификаторов записей по условию S = 'B', используя индекс для S.
3. полученные списки пересекаются и там ищется, обычно вложенными циклами. На это требуется время.

2)

1. для поиска записи используется один из индексов: или q, или S;
2. читаются записи;
3. результат определяется программно.

Преимущества B-деревьев:

• при обновлении записи в таблице блокируется только сама обновляемая запись;
• очень хорошо изучены, существуют эффективные алгоритмы реализации.

Недостатки B-деревьев:

• достаточно большой объём, занимаемый индексом;
• большое время выполнения операции со списком идентификаторов записи, удовлетворящих условию поиска.

Bit Mapped Index

Структура битового индекса такая же, как и у B-дерева. Отличаются они структурой записи блока листового уровня.

У битового индекса она такова:

<
    значение атрибута(ов) - mean,
    начальный идентификатор записи - start_rowid,
    конечный идентификатор записи - end_rowid,
    сегмент двоичной карты - bitmap_segment
>

Рассмотрим пример записи блока листового уровня индекса, построенного для некоторого атрибута q:

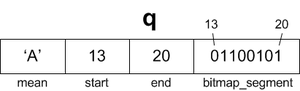
Эта запись означает, что 14, 15, 18 и 20 записи имееют значение атрибута q равное 'A'.

Определим количество блоков на листовом уровне.

Введём следующие обозначения:

$V$ - число записей в таблице БД;

$Lq$ - длина индексируемого атрибута;

$Lr$ - длина указателя на запись;

$Lb$ - длина сегмента bitmap.

Получаем числов блоков $$Q = \frac{V}{8\cdot Lb}\cdot (Lq + 2\cdot Lr + Lb)$$

Предположим, задана следующая таблица:

T1

...	q	S	...
...	'A'	'B'	...

И выдаётся запрос с условием

SELECT * FROM T1
WHERE q = 'A' AND S = 'B'

Предположим, что запись блока листового уровня для индекса по атрибуту q имеет вид 'A' 13 20 bitmap_segment1, а для индекса по атрибуту S имеет вид 'B' 13 20 bitmap_segment2.

Тогда при выполнении запроса СУБД использует индексы по обоим атрибутам. Для работы с пересечением битовых массивов используется всего одна ассемблерная команда - это очень быстро.

Также скорость проявляется при инвертировании условия запроса: если надо искать не равенство, а неравенство атрибута, то достаточно только инвертировать сегмент, а в B-дереве надо просматривать опять всю таблицу.

Преимущества битового индекса:

• занимает меньший объём, чем B-дерево;
• поиск записей по условиям выполняется быстрее, чем в B-деревьях.

Недостаток битового индекса:

• при обновлении одной записи блокируются все записи, связанные с сегментом. Если модифицируется 14 запись, то блокируются записи с 13 по 20, например.

продолжение...