ТОРА (9) - Лекция №8 - Алгоритм (продолжение)

...начало

Практические приёмы нормализации

Пример 1

Поэтому вновь перестроим схему:

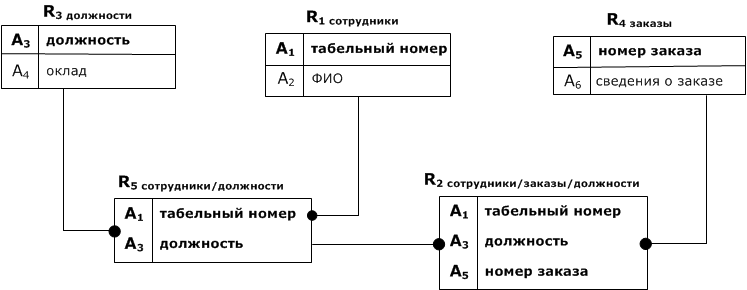
Указанная схема имеет два недостатка:

1. в ключи $R_3$, $R_1$ и $R_4$ входят атрибуты предметной области. При изменении формата табельного номера придётся обновить его в $R_1$ и через CASCADE в $R_3$ и $R_4$. Поэтому всегда желательно иметь синтетические ключи - не связанные с предметной областью (ID);
2. в сущностях $R_2$ и $R_5$ ключи составные. Это увеличивает размер индекса и время поиска по этому индексу.

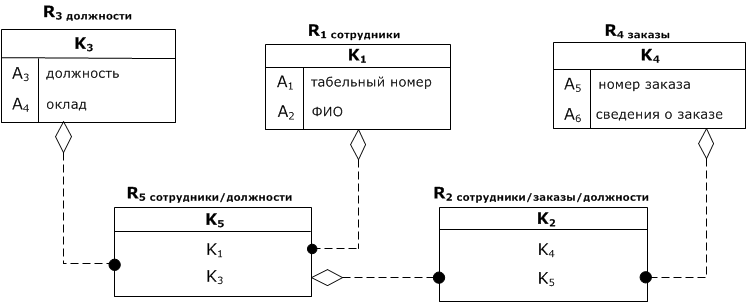
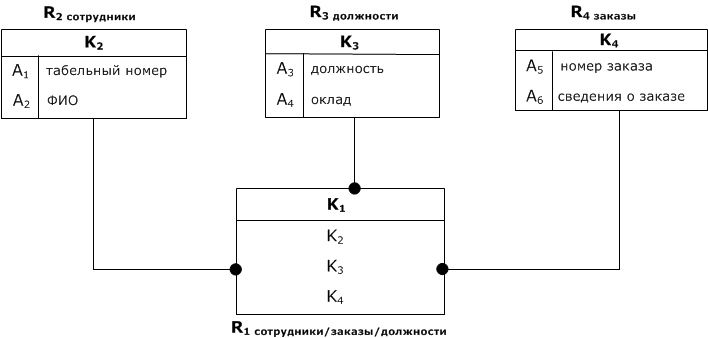
В силу этого, схему БД предлагается реорганизовать следующим образом (ввести синтетические ключи):

Пример 2

Разработать схему БД для предыдущего примера с применением алгоритма синтеза.

$U$ = (табельный номер, ФИО, должность, оклад, номер заказа, сведения о заказе) = $(A_1, A_2, A_3, A_4, A_5, A_6)$

$F = (A_1\rightarrow A_2, A_3\rightarrow A_4, A_5\rightarrow A_6)$

Синтез:

1)

$УНП = (A_1\rightarrow A_2, A_3\rightarrow A_4, A_5\rightarrow A_6)$

2)

$U\rightarrow\varnothing$

в УНП нет ФЗ, включающей все атрибуты из $U$. Поэтому добавляем в УНП тривиальную ФЗ:

$УНП = (A_1\rightarrow A_2, A_3\rightarrow A_4, A_5\rightarrow A_6, A_1 A_2 A_3 A_4 A_5 A_6\rightarrow\varnothing)$

3)

все нетривиальные ФЗ в УНП являются неприводимыми (в левой части один атрибут). Поэтому шаг пропускаем.

4)

разбиваем УНП на классы ФЗ:

1. $A_1\rightarrow A_2$, $K_1 = A_1 A_2$
2. $A_3\rightarrow A_4$, $K_2 = A_3 A_4$
3. $A_5\rightarrow A_6$, $K_3 = A_5 A_6$
4. $A_1 A_2 A_3 A_4 A_5 A_6\rightarrow\varnothing$, $K_4 = A_1 A_2 A_3 A_4 A_5 A_6$

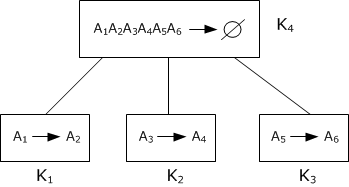
5)

строим граф иерархии:

6)

пропускаем, так как в каждом классе только одна ФЗ.

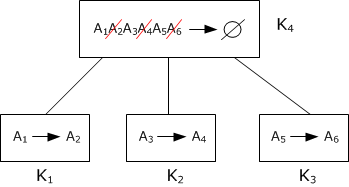
7)

выполняем редуцирование атрибутов ФЗ:

8)

пропускаем, так как в графе иерархии нет ФЗ, кроме $U\rightarrow\varnothing$

9)

$\rho = (A_1 A_3 A_5, A_1 A_2, A_3 A_4, A_5 A_6)$

10)

1) соединение без потерь

	$A_1$	$A_2$	$A_3$	$A_4$	$A_5$	$A_6$
$R_1$	$a$	$b_1$	$a$	$b_1$	$a$	$b_1$
$R_2$	$a$	$a$	$b_2$	$b_2$	$b_2$	$b_2$
$R_3$	$b_3$	$b_3$	$a$	$a$	$b_3$	$b_3$
$R_4$	$b_4$	$b_4$	$b_4$	$b_4$	$a$	$a$

	$A_1$	$A_2$	$A_3$	$A_4$	$A_5$	$A_6$
$R_1$	$a$	$a$	$a$	$a$	$a$	$a$
$R_2$	$a$	$a$	$b_2$	$b_2$	$b_2$	$b_2$
$R_3$	$b_3$	$b_3$	$a$	$a$	$b_3$	$b_3$
$R_4$	$b_4$	$b_4$	$b_4$	$b_4$	$a$	$a$

Получили строку, сплошь состоящую из $a$. Значит, есть соединение без потерь. Запрос на соединение всех четырёх таблиц будет выполняться правильно.

2) сохранение ФЗ:

1-4) $H = \varnothing$, $УНП = (A_1\rightarrow A_2, A_3\rightarrow A_4, A_5\rightarrow A_6)$

5) $H$ - пусто.

6) обладает сохранением ФЗ. При включении новой записи в таблицу достаточно проверять справедливость тех ФЗ, которые связаны с этой таблицей.

3) каждая схема отношения находится в 3НФ. Вот так.

А находятся ли схемы отношений $R_1, R_2, R_3, R_4$ в нормальной форме Бойса-Кодда?

$R_1$:

$R_1 = A_1 A_3 A_5$, $A_1 A_3 A_5$ - ключ, значит находится в НФБК.

$R_2$:

$R_2 = A_1 A_2$, $A_1\rightarrow A_2$, $A_1$ - ключ, значит находится в НФБК.

$R_3$:

$R_4 = A_3 A_4$, $A_3\rightarrow A_4$, $A_3$ - ключ, значит находится в НФБК.

$R_4$:

$R_4 = A_5 A_6$, $A_5\rightarrow A_6$, $A_5$ - ключ, значит находится в НФБК.

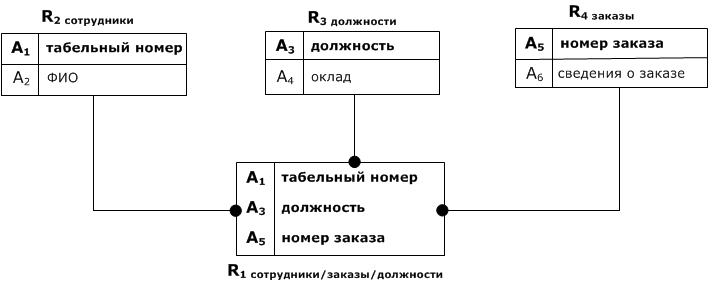
В конце концов, получаем такую схему БД:

Но у неё тоже есть недостатки:

1. ключ в $R_1$ составной;
2. в ключах $R_2, R_3, R_4$ используются атрибуты предметной области.

Перестроим схему с синтетическими ключами:

Сравнивая результаты Примера 1 и Примера 2, видим, что алгоритм синтеза даёт меньшее число схем отношений.