ТОРА (9) - Лекция №9 - Оптимизация запросов

Материал из Кафедра ИУ5 МГТУ им. Н.Э.Баумана - студенческое сообщество
Перейти к: навигация, поиск

Оригинал всего раздела, посвящённого оптимизации SQL-запросов, от самого Григорьева можно загрузить здесь.

Оптимизация SQL-запросов

Запрос, поступающий в СУБД, подвергается оптимизации с целью уменьшения времени его выполнения.

Шаги оптимизатора:

  1. строится логический план выполнения запроса (дерево логических операций);
  2. на основе логического плана строится физический план выполнения запроса (дерево физических операций);
  3. реализация этого физического плана.

Законы реляционной алгебры

Закон коммутативности декартова произведения отношений

$R_1\times R_2 = R_2\times R_1$, здесь и далее $R_1$ и $R_2$ - экземпляры отношений.

Закон ассоциативности декартова произведения

$(R_1\times R_2)\times R_3 = R_1\times (R_2\times R_3)$

Закон каскада проекций

Допустим, $(a_1 ... a_n)\subseteq (b_1 ... b_n)$, ${a_i}$, ${b_i}$ - это атрибуты отношения $R$

тогда $\Pi_{a_1 ... a_n}(\Pi_{b_1 ... b_n}(R)) = \Pi_{a_1 ... a_n}(R)$

Закон каскада селекций

Допустим, $F = f_1\wedge f_2$

тогда $\sigma_F(R) = \sigma_{f_1}(\sigma_{f_2}(R))$

Закон перестановки проекции и селекции

1)

Допустим, в условия поиска $F$ входят атрибуты только из множества $a_1 ... a_n$
тогда $\Pi_{a_1 ... a_n}(\sigma_F(R)) = \sigma_F(\Pi_{a_1 ... a_n}(R))$

2)

Допустим, в условия поиска $F$ входят атрибуты не только из множества $a_1 ... a_n$, но и из $b_1 ... b_n$
тогда $\Pi_{a_1 ... a_n}(\sigma_F(R)) = \Pi_{a_1 ... a_n}(\sigma_F(\Pi_{a_1 ... a_n, b_1 ... b_n}(R)))$

Селекция декартова произведения

Отношение $f_1$ содержит атрибуты только из отношения $R_1$

тогда $\sigma_{f_1}(R_1\times R_2) = \sigma_{f_1}(R_1)\times R_2$

Следствие:
пусть $F = f_1 \wedge f_2$ и в $f_1$ входят атрибуты $R_1$, а в $f_2$ входят из $R_2$,
тогда $\sigma_{F}(R_1\times R_2) = \sigma_{f_1}(R_1)\times \sigma_{f_2}(R_2)$
Доказательство:
$\sigma_{f_1 \wedge f_2}(R_1\times R_2) = \sigma_{f_1}(\sigma_{f_2}(R_1\times R_2)) = \sigma_{f_1}(\sigma_{f_2}(R_2\times R_1))=$
$= \sigma_{f_1}(R_1\times\sigma_{f_2}(R_2)) = \sigma_{f_1}(R_1)\times \sigma_{f_2}(R_2)$

Закон перестановки селекции и объединения

$\sigma_{F}(R_1\bigcup R_2) = \sigma_{F}(R_1)\bigcup\sigma_{F}(R_2)$

Закон перестановки селекции и разности отношений

$\sigma_{F}(R_1 - R_2) = \sigma_{F}(R_1) - \sigma_{F}(R_2)$

Закон перестановки проекции и декартова произведения

$b_1 ... b_n$ - это атрибуты отношения $R_1$

$c_1 ... c_k$ - это атрибуты отношения $R_2$

$\Pi_{b_1 ... b_n, c_1 ... c_k}(R_1\times R_2)$ = $\Pi_{b_1 ... b_n}(R_1)\times \Pi_{c_1 ... c_k}(R_2)$

Закон перестановки проекции и объединения

$\Pi_{a_1 ... a_n}(R_1\bigcup R_2) = \Pi_{a_1 ... a_n}(R_1)\bigcup\Pi_{a_1 ... a_n}(R_2)$

Оптимизация формул реляционной алгебры

Пусть условие $F = f_1 \wedge ... \wedge f_n$

Правила:

  1. переместить каждую селекцию внутрь декартова произведения, используя законы 1, 4, 6, 7, 8;
  2. переместить каждую проекцию внутрь декартова произведения, используя законы 1, 3, 5, 9, 10;
  3. по возможности скомбинировать каждый каскад селекции в одиночную селекцию и каждый каскад проекции в одиночную проекцию. Тогда всё можно будет сделать за один проход.

После выполнения этих трёх правил выражение $\Pi_A(\sigma_F(R_1\times ...\times R_n))$ преобразуется к виду:

$\Pi_A(\sigma_F($$\Pi_{A_1}(\sigma_{f_1}(R_1))$$\times ...\times$$\Pi_{A_n}(\sigma_{f_n}(R_n))$$))$, здесь каждый $\Pi_{A_i}(\sigma_{f_i}(R_i))$ - это подзапрос.

Суть в том, что сначала выполняются подзапросы, а они имеют намного меньшую размерность, чем исходная таблица, и время выполнения будет меньше, чем по исходной формуле $\Pi_A(\sigma_F(R_1\times ...\times R_n))$.

Логический план

Построение логического плана

Порядок построения:

  1. запрос преобразуется в формулу реляционной алгебры;
  2. выполняется преобразование (оптимизация) этой формулы.

Оператор SELECT (без агрегирования, группирования и удаления дубликатов) может быть представлен так:

$\Pi_A(\sigma_F(R_1\times ...\times R_n))$, где

от $R_1$ до $R_n$ - это декартово произведение отношений (таблиц), указанных за ключевым словом FROM;
$\sigma_F$ - это селекция кортежей декартова произведения в соответствии с условием, указанным за ключевым словом WHERE;
$\Pi_A$ - это проекция селекции на множество атрибутов A, указанных за ключевым словом SELECT

В чём суть такой логической оптимизации? Сначала надо выполнить декартово произведение, потом селекцию, потом проекцию - всё по порядку скобок в этом выражении. Потому что если таблица имеет большой размер, то это выражение будет выполняться очень долго.

Пример: найти фамилии поставщиков, поставляющих детали с названием "винт".

$\rho = (S, P, SP)$ 

SELECT фамилия
FROM S, P, SP
WHERE P.название = 'винт' AND
      S.номер_поставки = SP.номер_поставки AND
      SP.номер_детали = P.номер_детали;

$\Pi_{фамилия}(\sigma_{P.н="винт" \wedge S.н-п=SP.н-п \wedge SP.н-д=P.н-д}(S\times P\times SP))$

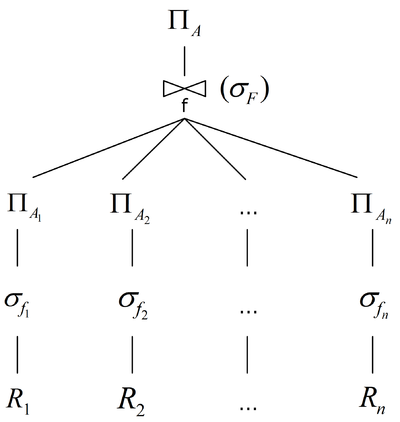
После преобразования и выделения подзапросов (как в описании, приведённом выше) получится выражение $\Pi_A(\sigma_F(\Pi_{A_i}(\sigma_{f_2}(R_1))\times ...\times \Pi_{A_n}(\sigma_{f_n}(R_n))))$, которое можно представить в графическом виде - это и будет логический план выполнения запроса:

9sTORAl9pic1.png

Получается, подзапросы можно выполнять параллельно, а это тоже уменьшает время выполнения всего запроса.

Пример:

9sTORAl9pic2.png

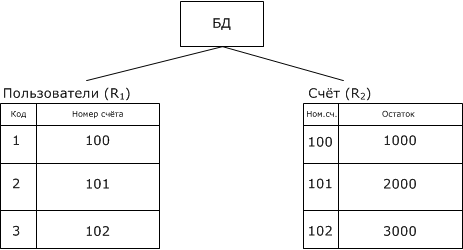
Запрос найти значение остатков больше 1500 на счетах пользователя с кодом 3: 

SELECT остаток
FROM R2
WHERE остаток > 1500 AND
      номер_счёта IN(
                     SELECT номер_счёта
                     FROM R1
                     WHERE код_пользователя = 3
                    );

Этот запрос преобразуется сервером в неявном виде в формулу реляционной алгебры:

$\Pi_{остаток}(\sigma_{R_2.о>1500 \wedge R_1.к-п=3 \wedge R_1.н-c=R_2.н-с}(R_1\times R_2))$

Теперь оптимизируем:

$=^4\Pi_{остаток}(\sigma_{R_1.н-c=R_2.н-с}(\sigma_{R_2.о>1500 \wedge R_1.к-п=3}(R_1\times R_2)))=^6$

$=\Pi_{остаток}(\sigma_{R_1.н-c=R_2.н-с}(\sigma_{R_1.к-п=3}(R_1)\times\sigma_{R_2.о>1500}(R_2)=^{5, 2}$

$=\Pi_{остаток}(\sigma_{R_1.н-c=R_2.н-с}(\Pi_{остаток, R_1.н-с, R_2.н-с}(\sigma_{R_1.к-п=3}(R_1)\times\sigma_{R_2.о>1500}(R_2))=^9$

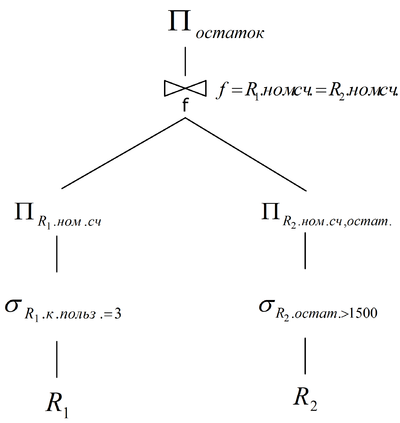
$=\Pi_{остаток}(\sigma_{R_1.н-c=R_2.н-с}($$\Pi_{R_1.н-с}(\sigma_{R_1.к-п=3}(R_1))$$\times$$\Pi_{R_2.н-с, остаток}(\sigma_{R_2.о>1500}(R_2))$$))$

Полученное выражение - результат оптимизации. Можно построить логический план выполнения запроса.

9sTORAl9pic3.png

Arrow right.png

продолжение...

Источник — «https://iu5bmstu.ru/index.php?title=ТОРА_(9)_-_Лекция_№9_-_Оптимизация_запросов&oldid=2637»