ТОРА (9) - Семинар №3 - Соединение без потерь
Свойства хорошей БД:
- соединение без потерь;
- сохранение ФЗ;
- нормализация схемы отношений (3НФ).
По этому семинару надо выполнить домашнее задание. В письменном виде в тетради.
Пример 1
Таблицы $$\rho=(S,P,SP)$$
- $$S$$ - поставщики.
- SN - номер поставщика;
- SF - фамилия;
- SS - статус;
- SG - город.
- $$P$$ - деталь.
- PN - номер детали, ключ;
- PF - название детали;
- PC - цена за единицу.
- $$SP$$ - поставка.
- SN - номер поставщика;
- PN - номер детали;
- kol - количество поставляемых деталей.
$$\rho = (S, P, SP)$$
Задачи:
- выписать ФЗ на основе знания предметной области;
- проверить, обладает ли $$\rho$$ соединением без потерь;
- проверить, обладает ли $$\rho$$ сохранением ФЗ;
- проверить, находится ли $$\rho$$ в 3НФ.
Задача 1
$$SN\rightarrow SF$$, $$SN\rightarrow SS$$, $$SN\rightarrow SG$$
$$PN\rightarrow PF$$, $$PN\rightarrow PC$$
$$SNPN\rightarrow kol$$
Задача 2
| SN | SF | SS | SG | PN | PF | PC | kol | |
|---|---|---|---|---|---|---|---|---|
| $$S$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ |
| $$P$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$a$$ | $$a$$ | $$b_2$$ |
| $$SP$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$a$$ |
| SN | SF | SS | SG | PN | PF | PC | kol | |
|---|---|---|---|---|---|---|---|---|
| $$S$$ | $$a$$ | $$a$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ |
| $$P$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$a$$ | $$a$$ | $$b_2$$ |
| $$SP$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
Получили строку, сплошь состоящую из $$a$$, значит $$\rho$$ обладает соединением без потерь - если мы соединим все три исходные таблицы, то получим правильный результат.
Задача 3
Обладает ли схема свойством созранения ФЗ?
1-4)
- $$H=\varnothing$$
- $$УНП = (SN\rightarrow SFSSSG, PN\rightarrow PFPC, SNPN\rightarrow kolSFSSSGPFPC)$$
- смотрим, кто принадлежит, получается:
- $$УНП = (SN\rightarrow SFSSSG, PN\rightarrow PFPC, SNPN\rightarrow kol)$$
- $$H = (SNPN\rightarrow SFSSSGPFPC)$$
5)
- $$H\neq\varnothing$$
6)
- выполняется ли $$SNPN\rightarrow SFSSSGPFPC\in (SN\rightarrow SFSSSG, PN\rightarrow PFPC, SNPN\rightarrow kol)^+$$?
- $$(SNPN)^+ = SNPNSFSSSGPFPCkol$$, значит выполняется, значит $$\rho$$ обладает сохранением ФЗ.
Задача 4
Находится ли отношение в 3НФ?
По каждой таблице.
Таблица S
Смотрим таблицу $$S$$:
1)
- $$X = SN$$ - ключ.
2)
- $$Y(Y\nrightarrow X)$$: $$SF, SS, SG, SFSS, SFSG, SSSG, SFSSSG$$
3)
- рассматриваем $$Y = SF$$, ищем такие $$H$$, которые не принадлежат $$Y$$: $$SS, SG$$
- а)
- $$SF\rightarrow SS$$?
- $$SF^+=SF$$, значит $$SS\notin SF^+$$
- б)
- $$SF\rightarrow SG$$?
- $$SF^+=SF$$, значит $$SG\notin SF^+$$
- и так далее, "рутинная тупая работа".
- А можно было, оказывается, так:
- Если для какого-либо $$Y$$ $$H\notin Y$$, то $$Y\nrightarrow H$$
- Доказательство: $$Y^+ = Y$$, а по условию $$H\notin (Y^+)$$, значит $$Y\nrightarrow H$$, так что таблица $$S$$ находится в 3НФ.
Таблица P
Таблица SP
Пример 2
Выписать все ФЗ.
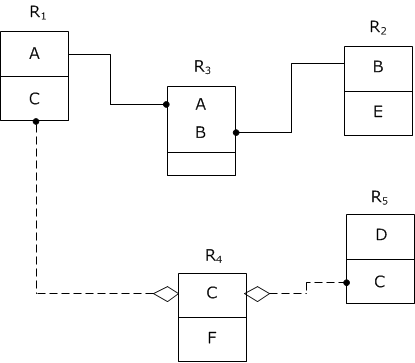
$$\rho = (R_1, R_2, R_3, R_4, R_5)$$
$$F = (A\rightarrow C, B\rightarrow E, C\rightarrow F, D\rightarrow C)$$
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ |
| $$R_5$$ | $$b_5$$ | $$b_5$$ | $$a$$ | $$a$$ | $$b_5$$ | $$b_5$$ |
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$a$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$a$$ | $$b_3$$ | $$a$$ | $$a$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ |
| $$R_5$$ | $$b_5$$ | $$b_5$$ | $$a$$ | $$a$$ | $$b_5$$ | $$a$$ |
Нет строчки, сплошь состоящей из $$a$$, значит $$\rho$$ не обладает соединением из потерь - запрос на соединение пяти таблицы может выполняться неправильно.
Смотрим:
SELECT *
FROM R1, R2, R3, R4, R5
WHERE R1.A = R3.A
AND R3.B = R2.B
AND R1.C = R4.C
AND R4.C = R5.C
и предположим, что задан следуюшие экземпляр универсальной схемы отношения:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$r$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$d_1$$ | $$e_1$$ | $$f_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$d_2$$ | $$e_2$$ | $$f_1$$ |
Найти проекции и выполнить их соединение по запросу выше.
Строим проекции:
$$r_1 = \Pi_{R_1}(r)$$
| A | C | |
|---|---|---|
| $$r_1$$ | $$a_1$$ | $$c_1$$ |
| $$a_2$$ | $$c_1$$ |
$$r_2 = \Pi_{R_2}(r)$$
| B | E | |
|---|---|---|
| $$r_2$$ | $$b_1$$ | $$e_1$$ |
| $$b_2$$ | $$e_2$$ |
$$r_3 = \Pi_{R_3}(r)$$
| A | B | |
|---|---|---|
| $$r_3$$ | $$a_1$$ | $$b_1$$ |
| $$a_2$$ | $$b_2$$ |
$$r_4 = \Pi_{R_4}(r)$$
| C | F | |
|---|---|---|
| $$r_4$$ | $$c_1$$ | $$f_1$$ |
$$r_5 = \Pi_{R_5}(r)$$
| D | C | |
|---|---|---|
| $$r_5$$ | $$d_1$$ | $$c_1$$ |
| $$d_2$$ | $$c_1$$ |
Теперь соединения:
$$t_1 = r_1 \bowtie_A r_3$$
| A | B | C | |
|---|---|---|---|
| $$t_1$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ |
$$t_2 = t_1 \bowtie_B r_2$$
| A | B | C | E | |
|---|---|---|---|---|
| $$t_2$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$e_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$e_2$$ |
$$t_3 = t_2 \bowtie_C r_4$$
| A | B | C | E | F | |
|---|---|---|---|---|---|
| $$t_3$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$e_1$$ | $$f_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$e_2$$ | $$f_1$$ |
$$t_4 = t_3 \bowtie_C r_5$$
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$t_4$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$d_1$$ | $$e_1$$ | $$f_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$d_1$$ | $$e_2$$ | $$f_1$$ | |
| $$a_1$$ | $$b_1$$ | $$c_1$$ | $$d_2$$ | $$e_1$$ | $$f_1$$ | |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$d_2$$ | $$e_2$$ | $$f_1$$ |
Получившееся не совпадает с исходной. Вот и проявилось отсутствие сохранения без потерь.
Но подсхемы $$(R_1, R_2, R_3, R_4)$$ и $$(R_4, R_5)$$, при этом, обладают соединением без потерь.
ДЗ
Задача №1
Находятся ли $$P$$ и $$SP$$ в 3НФ?
Таблица P
Ищем тройку:
- 1) $$X = PN$$, $$PN$$ - ключ.
- 2) $$Y(Y\nrightarrow X)$$: $$PF, PC, PFPC$$
- 3) рассматриваем:
- а) $$Y = PF$$, $$H\notin Y$$: $$PC$$
- $$PF\rightarrow^? PC$$ нет
- $$(PF)^+ = PF$$, $$PC\notin (PF)^+$$
- б) $$Y = PC$$, $$H\notin Y$$: $$PF$$
- $$PC\rightarrow^? PF$$ нет
- $$(PC)^+ = PC$$, $$PF\notin (PC)^+$$
- а) $$Y = PF$$, $$H\notin Y$$: $$PC$$
Таким образом, не удалось подобрать необходимую тройку, значит таблица находится в 3НФ.
Таблица SP
Ищем тройку:
- 1) $$X = PN SN$$, так как $$SN PN\rightarrow kol$$
- 2) подберём $$Y$$, для которого $$X\rightarrow Y$$, $$Y\rightarrow X$$, $$Y(Y\nrightarrow X)$$: $$kol$$
- $$(kol)^+ = kol$$, $$PNSN\nsubseteq kol$$, $$kol\nrightarrow SN$$
- 3) $$Y = kol$$ - нельзя подобрать непервичный атрибут $$H$$: $$H\notin Y$$
Таким образом, не удалось подобрать необходимую тройку, значит таблица находится в 3НФ.
Задача №2
Доказать, что эти две подсхемы $$(R_1, R_2, R_3, R_4)$$ и $$(R_4, R_5)$$ обладают соединением без потерь, и запрос на соединение выполнится правильно.
Ещё раз ФЗ: $$F = (A\rightarrow C, B\rightarrow E, C\rightarrow F, D\rightarrow C)$$
Первая подсхема
Подсхема $$(R_1, R_2, R_3, R_4)$$:
| A | B | C | E | F | |
|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$b_1$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$a$$ |
| A | B | C | E | F | |
|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$a$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$a$$ |
Получили строку, сплошь состоящую из $$a$$, значит подсхема $$(R_1, R_2, R_3, R_4)$$ обладает свойством соединения без потерь.
SELECT *
FROM R1, R2, R3, R4
WHERE R1.A = R2.A
AND R3.B = R2.B
AND R1.C = R4.C
Строим проекции:
$$r_1 = \Pi_{R_1}(r)$$
| A | C | |
|---|---|---|
| $$r_1$$ | $$a_1$$ | $$c_1$$ |
| $$a_2$$ | $$c_1$$ |
$$r_2 = \Pi_{R_2}(r)$$
| B | E | |
|---|---|---|
| $$r_2$$ | $$b_1$$ | $$e_1$$ |
| $$b_2$$ | $$e_2$$ |
$$r_3 = \Pi_{R_3}(r)$$
| A | B | |
|---|---|---|
| $$r_3$$ | $$a_1$$ | $$b_1$$ |
| $$a_2$$ | $$b_2$$ |
$$r_4 = \Pi_{R_4}(r)$$
| C | F | |
|---|---|---|
| $$r_4$$ | $$c_1$$ | $$f_1$$ |
Теперь соединения:
$$t_1 = r_1 \bowtie_A r_3$$
| A | B | C | |
|---|---|---|---|
| $$t_1$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ |
$$t_2 = t_1 \bowtie_B r_2$$
| A | B | C | E | |
|---|---|---|---|---|
| $$t_2$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$e_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$e_2$$ |
$$t_3 = t_2 \bowtie_C r_4$$
| A | B | C | E | F | |
|---|---|---|---|---|---|
| $$t_3$$ | $$a_1$$ | $$b_1$$ | $$c_1$$ | $$e_1$$ | $$f_1$$ |
| $$a_2$$ | $$b_2$$ | $$c_1$$ | $$e_2$$ | $$f_1$$ |
Соединение выполнилось верно.
Вторая подсхема
Подсхема $$(R_4, R_5)$$:
| C | D | F | |
|---|---|---|---|
| $$R_4$$ | $$a$$ | $$b_4$$ | $$a$$ |
| $$R_5$$ | $$a$$ | $$a$$ | $$b_5$$ |
| C | D | F | |
|---|---|---|---|
| $$R_4$$ | $$a$$ | $$a$$ | $$a$$ |
| $$R_5$$ | $$a$$ | $$a$$ | $$a$$ |
Получили строку, сплошь состоящую из $$a$$, значит подсхема $$(R_4, R_5)$$ обладает свойством соединения без потерь.
SELECT *
FROM R4, R5
WHERE R4.C = R5.C
Строим проекции:
$$r_4 = \Pi_{R_4}(r)$$
| C | F | |
|---|---|---|
| $$r_4$$ | $$c_1$$ | $$f_1$$ |
$$r_5 = \Pi_{R_5}(r)$$
| D | C | |
|---|---|---|
| $$r_5$$ | $$d_1$$ | $$c_1$$ |
| $$d_2$$ | $$c_1$$ |
Теперь соединение:
$$t_1 = r_4 \bowtie_C r_5$$
| C | D | F | |
|---|---|---|---|
| $$t_1$$ | $$c_1$$ | $$d_1$$ | $$f_1$$ |
| $$c_1$$ | $$d_2$$ | $$f_1$$ |
Соединение выполнилось верно.
Задача №3
Как минимальным образом изменить схему БД из примера 2, чтобы она обладала свойством соединения без потерь (чтобы запрос на соединение 5 таблиц выполнялся правильно).
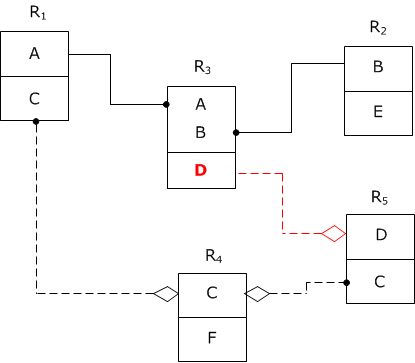
Изменяем схему:
Однако, это не самый минимальный способ, потому что мы ввели новую ФЗ. Можно было $$D$$ добавить в ключ, тогда связь была бы идентифицирующая.
Но так тоже можно.
Теперь:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$b_3$$ | $$a$$ | $$b_3$$ | $$b_3$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ |
| $$R_5$$ | $$b_5$$ | $$b_5$$ | $$a$$ | $$a$$ | $$b_5$$ | $$b_5$$ |
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| $$R_1$$ | $$a$$ | $$b_1$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$a$$ |
| $$R_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$R_3$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
| $$R_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ |
| $$R_5$$ | $$b_5$$ | $$b_5$$ | $$a$$ | $$a$$ | $$b_5$$ | $$a$$ |
Получили строку, сплошь состоящую из $$a$$, значит схема обладает свойством соединения без потерь.
Задача №4
Задана универсальная схема отношений:
$$R = (A, B, C, D, E, K, V, S, X, G)$$
Задано множество ФЗ:
$$F = (A\rightarrow BCDV, K\rightarrow D, V\rightarrow SX, V\rightarrow G, XG\rightarrow KEV, VX\rightarrow G)$$
Задана схема БД:
$$\rho = (AKE, ABCX, AVGX, VSDG)$$
Обладает ли эта схема БД свойством соединения без потерь и свойством сохранения ФЗ.
Соединение без потерь
$$\rho = (AKE, ABCX, AVGX, VSDG)$$
$$F = (A\rightarrow BCDV, K\rightarrow D, V\rightarrow SX, V\rightarrow G, XG\rightarrow KEV, VX\rightarrow D)$$
| $$A$$ | $$B$$ | $$C$$ | $$D$$ | $$E$$ | $$K$$ | $$V$$ | $$S$$ | $$X$$ | $$G$$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| $$AKE$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ | $$a$$ | $$a$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ | $$b_1$$ |
| $$ABCX$$ | $$a$$ | $$a$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$b_2$$ |
| $$AVGX$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ | $$b_3$$ | $$a$$ | $$b_3$$ | $$a$$ | $$a$$ |
| $$VSDG$$ | $$b_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$a$$ | $$b_4$$ | $$a$$ |
| $$A$$ | $$B$$ | $$C$$ | $$D$$ | $$E$$ | $$K$$ | $$V$$ | $$S$$ | $$X$$ | $$G$$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| $$AKE$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
| $$ABCX$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$b_2$$ | $$b_2$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
| $$AVGX$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ | $$b_3$$ | $$b_3$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
| $$VSDG$$ | $$b_4$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$b_4$$ | $$b_4$$ | $$a$$ | $$a$$ | $$a$$ | $$a$$ |
Получили строку, сплошь состоящую из $$a$$, значит $$\rho$$ обладает соединением без потерь.
Сохранение ФЗ
1-4)
- $$H = \varnothing$$
- $$УНП = A\rightarrow ABCDVSXGKE, K\rightarrow KD, V\rightarrow VSXGKED, XG\rightarrow XGKEVDS, VX\rightarrow VXDSGEK)$$
- $$H = (A\rightarrow S, K\rightarrow D, V\rightarrow KE, XG\rightarrow KEDS, VX\rightarrow DSEK)$$
5)
- $$H\neq\varnothing$$
6)
- $$H\in^? (A\rightarrow BCV, V\rightarrow SXG)$$ нет
$$A\rightarrow DS$$, $$A^+ = ABCVSXG$$
$$DS\notin ABCVSXG$$, значит $$\rho$$ не обладает сохранением ФЗ.