ТОРА (9) - Семинар №4 - Синтез хорошей БД

Синтез хорошей схемы БД

Из семинара 2: предметную область зададим следующую: "график полётов".

График = (пилот, рейс, дата, время), сокращённо: $\rho=(A,B,C,D)$

Итоговая $F = (B\rightarrow D, D\rightarrow B, BC\rightarrow A)$

Идём по алгоритму:

1)

строим условно-неизбыточное покрытие:

$УНП = B\rightarrow D, D\rightarrow B, BC\rightarrow AD$

2)

пропускаем, потому что есть $BC\rightarrow AD$

3)

$B\rightarrow^? AD$ нет

$B:+ = BD$, $AD\nsubseteq B^+$

$C\rightarrow^? AD$ нет

$C:+ = C$, $AD\nsubseteq C^+$

УНП остаётся без изменений.

4)

разбиваем на классы:

$B\rightarrow D$, $D\rightarrow B$, $K_1 = BD$

$BC\rightarrow AD$, $K_2 = BCAD$

5)

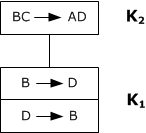
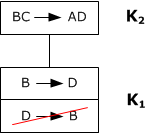
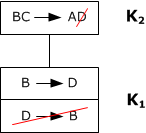
построить граф:

6)

7)

8)

пропускаем, потому что нет ФЗ с пустой правой частью.

9)

$\rho = (BD, ABC) = (R_1, R_2)$

10)

• смотрим соединение без потерь:

	$A$	$B$	$C$	$D$
$R_1$	$b$	$a$	$b$	$a$
$R_1$	$a$	$a$	$a$	$b$

	$A$	$B$	$C$	$D$
$R_1$	$b$	$a$	$b$	$a$
$R_1$	$a$	$a$	$a$	$a$

Есть строка сплошь из $a$, значит схема обладает соединением без потерь.

• смотрим сохранение ФЗ:

1-4) $H = \varnothing$, $УНП = (B\rightarrow B\rightarrow D, BC\rightarrow AD, D\rightarrow B)$

5) $H$ не пусто.

6)

$BC\rightarrow^? D\in(B\rightarrow D, BC\rightarrow A, D\rightarrow B)^+$

$(BC)^+ = BCAD$, $D\in (BC)^+$, значит, схема обладает сохранением ФЗ.

Таким образом, $\rho$ обладает соединением без потерь, сохранением ФЗ и находится в 3НФ.

ДЗ

Задание:

Проверить, находятся ли получившиеся $R_1$ и $R_2$ в НФБК?

Решение:

$\rho = (BD, ABC) = (R_1, R_2)$

$F = (B\rightarrow D, BC\rightarrow A)$

Отношение находится в НФБК, если для каждой нетривиальной и неприводимой ФЗ $X\rightarrow Y$ $X$ - ключ.

1. Выбираем ключи:

$R_1$:

1)

$i = 0$, $X_0 = BD$

$(X_0 - D)^+ = B^+ = BD = R$, $i = 1$, $X_1 = B$

$(X_0 - B)^+ = D^+ = D\neq R$

$i$ возросло.

2)

$i = 1$, $X_1 = B$

$(X_1 - B)^+ = \varnothing^+ = \varnothing$

$i$ не возросло, значит $B$ - ключ.

$R_2$:

1)

$i = 0$, $X_0 = ABC$

$(X_0 - A)^+ = (BC)^+ = ABC = R$, $i = 1$, $X_1 = BC$

$(X_0 - B)^+ = (AC)^+ = AC\neq R$

$(X_0 - C)^+ = (AB)^+ = AB\neq R$

$i$ возросло.

2)

$i = 1$, $X_1 = BC$

$(X_1 - B)^+ = C^+ = C\neq R$

$(X_1 - C)^+ = B^+ = B\neq R$

$i$ не возросло,значит $BC$ - ключ.

2. Проверяем:

$R_1$:

$B\rightarrow D$ - нетривиальная;

$\varnothing\subset B$, значит $B\rightarrow D$ - неприводимая;

$B$ - ключ, значит $R_1$ находится в НФБК.

$R_2$:

$BC\rightarrow A$ - нетривиальная;

$B\subset BC$, но $B\nrightarrow A$;

$C\subset BC$, но $C\nrightarrow A$;

выходит, $BC\rightarrow A$ ещё и неприводимая;

$BC$ - ключ, значит $R_2$ тоже находится в НФБК.