ТОРА (9) - Семинар №5 - Синтез хорошей БД

Алгоритм синтеза хорошей БД

Предметная область "Автовокзал".

Задана универсальная схема отношений:

$U =$

$($

$A$ - номер рейса автобуса,

$B$ - город назначения,

$C$ - дата отправления,

$D$ - время отправления,

$E$ - гос.номер автобуса,

$R$ - модель автобуса,

$K$ - ФИО водителя,

$L$ - дата рождения водителя,

$M$ - домашний адрес водителя,

$N$ - телефон водителя,

$X$ - ФИО пассажира автобуса,

$Y$ - место пассажира в автобусе,

$W$ - номер билета пассажира,

$V$ - цена билета,

$P$ - номер паспорта

$)$

Заданы ФЗ:

$K\rightarrow LMN, E\rightarrow R, A\rightarrow BD, AC\rightarrow KE, CDK\rightarrow A, P\rightarrow X, W\rightarrow ACVYP, BCD\rightarrow AK, BRY\rightarrow V$

Синтезировать схему БД, используя алгоритм.

1)

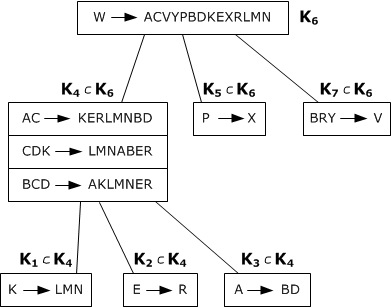
$УНП = (K\rightarrow LMN, E\rightarrow R, A\rightarrow BD, AC\rightarrow KERLMNBD,$

$CDK\rightarrow LMNABKER, P\rightarrow X, W\rightarrow ACVYPBDKEXRLMN, BCD\rightarrow AKLMNER,$

$BRY\rightarrow V)$

2)

есть ФЗ $W\rightarrow ACVYPBDKEXRLMN$, объединение левой и правой частей которой даёт все атрибуты. Пропускаем шаг.

3)

$A^+ = ABD$, $C^+ = C$, потому $AC\rightarrow KERLMNBD$ оставляем в покое.

$D^+ = D$, $K^+ = KLMN$

$(CD)^+ = CD$, $(DK)^+ = DKLMN$, $(CK)^+ = CKLMN$

$B^+ = B$, $(BC)^+ = BC$, $(BD)^+ = BD$

$R^+ = R$, $Y^+ = Y$, $(BR)^+ = BR$, $(RY)^+ = RY$, $(BY)^+ = BY$

таким образом, все зависимости из УНП неприводимые.

4)

разбиваем на классы эквивалентности (у кого совпадают объединения левой и правой части):

$K\rightarrow LMN$, $K_1 = KLMN$

$R\rightarrow R$, $K_2 = ER$

$A\rightarrow BD$, $K_3 = ABD$

$AC\rightarrow KERLMNBD$

$CDK\rightarrow LMNABER$

$BCD\rightarrow AKLMNER$

$K_4 = ACKERLMNBD$

$P\rightarrow X$, $K_5 = PX$

$W\rightarrow ACVYPBDKEXRLMN$, $K_6 = WACVYPBDKEXRLMN$

$BRY\rightarrow V$, $K_7 = BRYV$

5)

6)

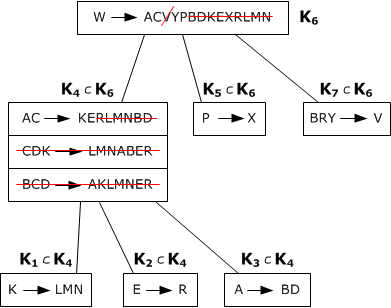
в каждом классе должна остаться только одна ФЗ:

$AC\rightarrow K$

$CDK\rightarrow AB$

$BCD\rightarrow AK$

Вычёркиваем лишнее, выбираем ФЗ с наименьшим числом атрибутов слева.

7)

Перерисуем без вычеркнутых:

8)

пропускаем, так как нет ФЗ с пустой правой частью.

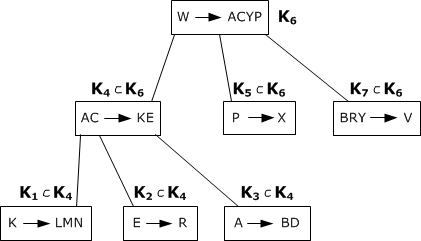
9)

$\rho = (WACYP, ACKE, KLMN, ER, ABD, PX, BRYV) = (R_1, R_2, R_3, R_4, R_5, R_6, R_7)$

10)

• смотрим соединение без потерь:

	$A$	$B$	$C$	$D$	$E$	$R$	$K$	$L$	$M$	$N$	$X$	$Y$	$W$	$V$	$P$
$R_1$	$a$		$a$									$a$	$a$		$a$
$R_2$	$a$		$a$		$a$		$a$
$R_3$							$a$	$a$	$a$	$a$
$R_4$					$a$	$a$
$R_5$	$a$	$a$		$a$
$R_6$											$a$				$a$
$R_7$		$a$				$a$						$a$		$a$

	$A$	$B$	$C$	$D$	$E$	$R$	$K$	$L$	$M$	$N$	$X$	$Y$	$W$	$V$	$P$
$R_1$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$	$a$
$R_2$	a	$a$	a	$a$	a	$a$	a	$a$	$a$	$a$
$R_3$							$a$	$a$	$a$	$a$
$R_4$					$a$	$a$
$R_5$	$a$	$a$		$a$
$R_6$											$a$				$a$
$R_7$		$a$				$a$						$a$		$a$

есть строка сплошь состоящая из $a$, значит $\rho$ обладает соединением без потерь.

• смотрим сохранение ФЗ:

1-4) $H = \varnothing$, $УНП = (K\rightarrow LMN, E\rightarrow R, A\rightarrow BD, AC\rightarrow KE, P\rightarrow X, W\rightarrow ACYP, BRY\rightarrow V)$

5) переписываем ФЗ, которые повычёркивали. $H\neq\varnothing$;

6)

$AC\rightarrow^? RLMNBD$ да

$(AC)^+ = ACBDKERLMN$

$CDK\rightarrow^? LMNABER$ нет

$(CDK)^+ = CDKLMN$

раз хотя бы одно нет, то вся $\rho$ не обладает сохранением ФЗ. Но это не страшно, если исходные данные вводятся с учётом здравого смысла.

Каждая схема отношения из $\rho$ уже находится в 3НФ. Покажем, что эти схемы отношения находятся ещё и в НФБК:

1. $R_1 = WACYP$, $W\rightarrow ACVYP$, $W$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
2. $R_2 = ACKE$, $AC\rightarrow KE$, $AC$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
3. $R_3 = KLMN$, $K\rightarrow LMN$, $K$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
4. $R_4 = ER$, $E\rightarrow R$, $E$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
5. $R_5 = ABD$, $A\rightarrow BD$, $A$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
6. $R_6 = PX$, $P\rightarrow X$, $P$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК;
7. $R_7 = BRYV$, $BRY\rightarrow V$, $BRY$ - ключ, а ФЗ неприводимая и нетривиальная, значит отношение в НФБК.

ДЗ 1

Задание:

1. По этой же схеме $\rho$ построить диаграмму сущность-связь по нотации ERwin, используя идентифицирующие и неидентифицирующие связи;
2. Выявить недостатки этой диаграммы:
   1. в $R_6$ ключ $P$ является составным ключом (номер, серия, кем выдан паспорт);
   2. в $R_2$ и $R_7$ ключи тоже составные;
   3. в ключи входят атрибуты предметной области (это плохо).

Поэтому диаграмму надо будет перерисовать, используя синтетические ключи.

ДЗ 2

Первая задача

Задание:

Задана предметная область про пилотов, но ФЗ другие:

$F = (B\rightarrow D, D\rightarrow B, AB\rightarrow D, AD\rightarrow B, BC\rightarrow A, BC\rightarrow D, CD\rightarrow A, CD\rightarrow B,$ $ABC\rightarrow D, ACD\rightarrow B, BCD\rightarrow A)$

Синтезировать БД с помощью алгоритма.

Вторая задача

Задание:

Новая предметная область: курсы иностранных языков.

$U =$

$($

$A$ - код курса,

$B$ - код филиала,

$C$ - условия обучения,

$D$ - номер группы (состоит из номера филиала и номера группы),

$E$ - номер уровня обучения,

$K$ - ФИО слушателя,

$L$ - число оплаченных слушателем занятий (оплачиваются все занятия курса сразу),

$N$ - стоимость обучения для студентов и школьников,

$O$ - стоимость обучения для взрослых,

$P$ - адрес филиала,

$R$ - заведующий филиалом,

$S$ - телефон филиала,

$T$ - часы работы преподавателя с группой слушателей (количество часов),

$V$ - зарплата преподавателя,

$X$ - ФИО преподавателя

$)$

ФЗ:

$F = (A\rightarrow CNO, B\rightarrow PRS, ADE\rightarrow X, K\rightarrow DEL, L\rightarrow T, X\rightarrow VT, ET\rightarrow V, D\rightarrow XBE)$

Синтезировать схему БД по алгоритму. Со следующими свойствами:

• соединение без потерь;
• каждая схема в 3НФ;
  • каждую проверить ещё и на НФБК;
• наименьшее число схем отношений;
• сохранение ФЗ (если не обладает, то новых схемы отношений добавлять не надо).

продолжение...