АМСОИ (10) - Лекция №6 - Анализ СМО с отказом
Оценка характеристик функционирования систем с отказом
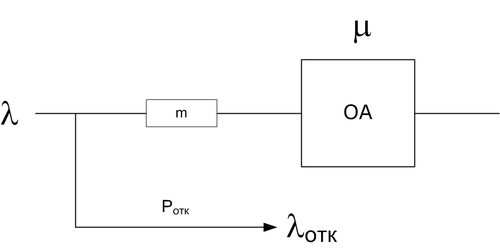
$$\lambda = \mu$$
$$\rho = \frac{\lambda}{\mu} = 1$$
Количество состояний системы $$m + 2$$
Поскольку $$\lambda = \mu$$, то все состояния равновероятны.
Вероятность отказа: $$$P_{отк} = P_{m+1} = \frac{1}{m+2} $$$
Интенсивность отказа: $$$\lambda_{отк} = \lambda\cdot P_{отк} = \frac{\lambda}{m + 2} $$$
Поток заявок, попадающий в систему: $$$\lambda_{обсл} = \lambda - \lambda_{отк} = \lambda\cdot (1 - \frac{1}{m+2}) = \frac{m + 1}{m + 2}\cdot\lambda$$$
$$$\lambda_{вых} = \lambda_{обсл} $$$
Коэффициент использования ОА: $$$U = \sum_{i=1}^{m+1} P_i = 1 - P_0 = 1 - \frac{1}{m+2} = \frac{m + 1}{m + 2} $$$
Количество заявок в очереди: $$$Q = \sum_{i=1}^{m+1} (i - 1)\cdot P_i = \sum_{i=1}^{m+1} i\cdot P_i - \sum_{i=1}^{m+1} P_i = \frac{1}{m + 2}\cdot\sum_{i=1}^{m+1} i - \sum_{i=1}^{m+1} P_i = \frac{m}{2}\cdot\frac{m+1}{m+2} $$$
Количество заявок в системе (с учётом, что у нас есть отказы): $$$L = Q + U$$$
Если бы не было отказов, то было бы: $$$L = Q + \rho$$$
Ещё способ: $$$L = \sum_{i=1}^{m+1} i\cdot P_i = \frac{1}{m+2}\cdot\sum_{i=1}^{m+1} = \frac{m+1}{2} $$$
Среднее время ожидания $$W$$ определяется тремя способами:
- учитываются и заявки отказа (у них время ожидания 0), и попавшие в систему. Время получится наименьшим;
- все заявки, попадающие в систему, но заявки, не ждущие в очереди, тоже учитываются. Время ожидания получится больше, чем в первом способе;
- все заявки, попадающие в систему. Заявки, не ждущие в очереди, не учитываются. Время ожидания получится наибольшим из трёх способов.
$$$W = \frac{Q}{\lambda_{обсл} } = \frac{m}{2}\cdot\frac{(m+1)\cdot (m+2)}{(m+2)\cdot(m+1)\cdot\mu} = \frac{m}{2\cdot\mu} $$$
Среднее время пребывания в системе: $$$T = \frac{L}{\lambda_{обсл} } = \frac{m+2}{2\cdot\mu} $$$
Относительная пропускная способность СМО: $$$q = \frac{\lambda_{обсл} }{\lambda} = \frac{m+1}{m+2} $$$
Абсолютная пропускная способность СМО (поток, который поступает в систему): $$$A = q\cdot\lambda$$$
Для определения числа мест в буфере $$m$$ можно ориентировочно пользоваться следующей приближённой формулой: $$$m = \frac{\rho - 2\cdot P_{отк} }{P_{отк} } $$$
Домашнее задание №4
Рассчитать характеристики одноканальной СМО (в которой происходят отказы в обслуживании, как и у рассматриваемой на лекции). Исходные данные у всех групп разные:
- $$\rho = 0.9$$, $$m = 0..10$$;
- $$\rho = 0.5$$, $$m = 0..10$$;
- $$\rho = 0.6$$, $$m = 0..10$$;
- $$\rho = 0.8$$, $$m = 0..10$$.
Найти вероятность $$P_{отк}$$.
Написать на GPSS модель этой системы. Поток пуассоновский, обслуживание экспоненциальное.