ТОРА (9) - Лекция №11 - Оценки
...начало

Оригинал всего раздела, посвящённого оптимизации SQL-запросов, от самого Григорьева можно загрузить здесь.
Оптимизация SQL-запросов
Физический план
Методы выбора записей из исходной таблицы
Оценка числа кортежей в промежуточной таблице
В таблице $$Q$$. Вычисляется по формуле:
$$Q = \Pi_A(\sigma_f(R))$$
$$T(Q) = T(R)\cdot p$$
здесь:
- $$Q$$ - промежуточная таблица;
- $$T(Q)$$ - число кортежей в промежуточной таблице;
- $$T(R)$$ - число записей в исходной таблице $$R$$;
- $$p$$ - вероятность того, запись из таблицы $$R$$ удовлетворяет условию $$F$$.
Расчёт $$p$$:
- если $$f = F_1\bigcap F_2$$, то $$p = p_1\cdot p_2$$;
- если $$f= F_1\bigcup F_2$$, то $$p = p_1 + p_2 - p_1\cdot p_2$$;
- если $$f = \overline{F_1}$$, то $$p = 1 - p_1$$.
Для $$i$$-ой вероятности:
$$p_i = \frac{k}{I(R,a)}$$
здесь:
- $$k$$ - мощность атрибута $$a$$ в запросе;
- $$I(R,a)$$ - мощность атрибута $$a$$ в таблице $$R$$.
Пример
Допустим, $$T(R) = 1000$$, $$I(R,a) = 5$$, $$I(R,b) = 10$$, $$I(R,c) = 2$$, где $$a,b,c$$ - положительные натуральные числа.
И $$f = (a<3$$ $$OR$$ $$b\geq5)$$ $$AND$$ $$c=2$$
Найти $$T(Q)$$.
Обозначим:
- $$a<3$$ как $$F_1$$;
- $$b\geq 5$$ как $$F_2$$;
- $$f = (a<3$$ $$OR$$ $$b\geq5)$$ как $$F_3$$;
- $$c=2$$ как $$F_4$$.
1)
- $$F_1\bigcup F_2 = F_3$$
- $$p_3 = p_1 + p_2 - p_1\cdot p_2 = \frac{2}{5} + \frac{6}{10} - \frac{2}{5}\cdot\frac{6}{10} = 0.76$$
2)
- $$f = F_3\bigcap F_4$$
- $$p = p_3\cdot p_4 = 0.76\cdot\frac{1}{2} = 0.38$$ - это вероятность того, что запись из $$R$$ удовлетворяет условию $$f$$.
3)
- $$T(Q) = 1000\cdot 0.38 = 380$$
Оценка количества блоков
$$Q = \Pi_A(\sigma_f(R))$$
$$B(Q) = \Bigr[\frac{T(Q)}{L_B}\Bigl]$$ - скобки обзначают, что огругление с избытком.
здесь:
- $$T(Q)$$ - прогнозируемое число записей в подзапросе;
- $$L_B$$ - длина блока (число записей в блоке) с учётом $$\Pi_A$$.
Порядок соединения промежуточных таблиц
Деревья соединения
Используются деревья соединения, которые бывают трёх видов:
- левостороннее;
- кустовое, ветвящееся;
- правостороннее.
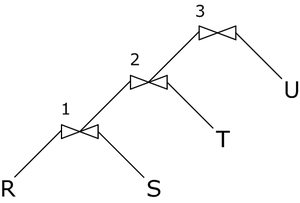
Левостороннее
Предположим, соединяются таблицы $$R,S,T,U$$:
В каждом соединении правым аргументом является одна из таблиц.
Преимущества:
- число перебора вариантов меньше, чем для произвольного варианта соединения (если количество соединений $$n$$, то вариантов перебора будет $$n!$$);
- достаточно просто организивать каналы обработки - возможность передачи результата выполнения одной операции на вход другой через оперативную память (без сохранения на диск);
В канале левый аргумент называется опорным и он должен храниться в оперативной памяти. Правый аргумент называется тестируемым и он может храниться и на диске. При хранении в оперативной памяти не надо читать с диска, потому всё можно выполнить за один проход.
Недостатки:
- путём перебора порядков соединения можно выбрать квазиоптимальный план (потому что на самом деле вариантов перебора больше, чем $$n!$$, потому что правый аргумент - всегда таблица).
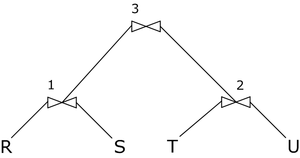
Кустовое
Тут таблицы могут соединяться в любом порядке.
Так что перебираются все возможные варианты соединения.
Преимущества:
- всегда выбирается оптимальный план.
Недостатки:
- если количество соединяемых таблиц велико, то перебор всех деревьев может занять много времени;
- могут возникнуть сложности в организации канала обработки, так как возрастают требования к объёму оперативной памяти. Чтобы реализовать соединение за один проход, в памяти должно храниться слишком много таблиц.
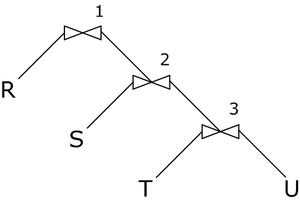
Правостороннее
При таком порядке левым аргументом каждого соединения является исходная таблица.
Такой способ практически не используется, потому что для него требуется, чтобы каждая из исходных таблиц и промежуточные результаты могли уместиться в оперативной памяти.
Методы соединения таблиц
Методы реализации естественного соединения $$\bowtie$$.
Три метода:
- вложенных циклов (NLJ - Nested Loop Join);
- сортировки слияния (SMJ - Sort Merge Join);
- хэшированных соединений (Hash Join).
продолжение...