ТОРА (9) - Семинар №8 - Пример решения ДЗ на оптимизацию запроса

Пример решения ДЗ №3

Это не само решение, а только разбор похожей задачи. И тот не до конца.

Предметная область

$$S$$ - таблица "Поставщик", описывающая поставщиков деталей. Имеет следующие поля:

• номер поставщика - идентификационный номер поставщика (ключевое поле);
• имя - фамилия, имя и отчество поставщика;
• состояние - состояние поставщика (состояние счета);
• город - город, в котором проживает поставщик и в котором находится его центральный офис.

$$P$$ - таблица "Деталь". Описывает поставляемые детали и включает следующие поля:

• номер детали - идентификационный номер детали (ключевое поле);
• название - название детали;
• цвет - цвет детали;
• вес - все детали в фунтах;
• город - город, в котором изготавливается деталь.

$$J$$ - таблица "Изделие". Описывает изготавливаемые изделия и включает следующие поля

• номер изделия - идентификационный номер изделия (ключевое поле);
• название - название изделия;
• город - город, где изготавливается изделие.

$$SPJ$$ - таблица "Сборка". Имеет следующие поля:

• номер поставщика — идентификационный номер поставщика, поставляющего деталь (ключевое поле);
• номер детали - идентификационный номер детали, поставляемой поставщиком (ключевое поле);
• номер изделия - идентификационный номер изделия, в которое входит деталь, поставляемая поставщиком (ключевое поле);
• количество - количество деталей, поставляемых поставщиком для данного изделия (количество деталей в поставке).

Диаграмма сущность-связь:

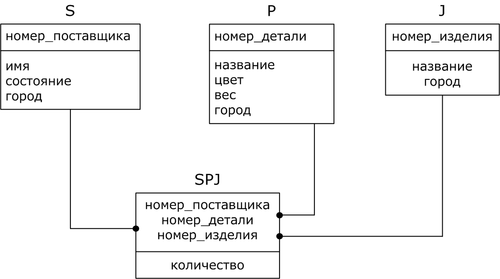
Запрос

Поступает запрос: "Найти название изделий, изготавливаемых в Париже и содержащих детали с названием "винт"". В запросе участвуют таблицы Деталь, Изделие и Сборка.

SELECT J.название
FROM P, J, SPJ
WHERE J.город = 'Париж' AND P.название = 'винт'
      AND J.ном_изд = SPJ.ном_изд AND P.ном_дет = SPJ.ном_дет;

Преобразовать этот запрос в форму реляционной алгебры:

$$\Pi_{назв\_ изд}(\sigma_{J.город = Париж\wedge P.название = винт\wedge J.ном\_ изд = SPJ.ном\_ изд\wedge P.ном\_ дет = SPJ.ном\_ дет}(P\times J\times SPJ)) =$$

применяем закон каскада селекций:

$$= \Pi_{назв\ _изд}(\sigma_{J.ном\_ изд = SPJ.ном_изд\wedge P.ном\_ дет = SPJ.ном\_ дет}(\sigma_{J.город = Париж\wedge P.название = винт}(P\times J\times SPJ))) =$$

применяем закон селекции декартова произведения:

$$= \Pi_{назв\_ изд}(\sigma_{J.ном\_ изд = SPJ.ном\_ изд\wedge P.ном\_ дет = SPJ.ном_дет}(\sigma_{J.город = Париж}(J)\times\sigma_{P.название = винт}(P)\times SPJ)) =$$

применяем закон перестановки проекции и селекции:

$$= \Pi_{назв\_ изд}(\sigma_{J.ном\_ изд = SPJ.ном\_ изд\wedge P.ном\_ дет = SPJ.ном\_ дет}(\Pi_{J.название, J.ном\_ изд, SPJ.ном\_ изд, P.ном\_ дет, SPJ.ном\_ дет,J.город = Париж}(J)\times$$

$$\times\sigma_{P.название = винт}(P)\times SPJ)) =$$

применяем закон перестановки проекции и декартова произведения:

$$= \Pi_{назв\_ изд}(\sigma_{J.ном\_ изд = SPJ.ном\_ изд\wedge P.ном\_ дет = SPJ.ном\_ дет}($$

$$\Pi_{J.название, J.ном\_ изд}(\sigma_{J.город = Париж})$$$$\times$$

$$\times$$$$\Pi_{P.ном\_ дет}(\sigma_{P.название = винт})$$$$\times$$

$$\times$$$$\Pi_{SPJ.ном\_ изд, SPJ.ном\_ дет}(SPJ)$$$$))$$

Каждая из проекций - подзапрос.

Логический план

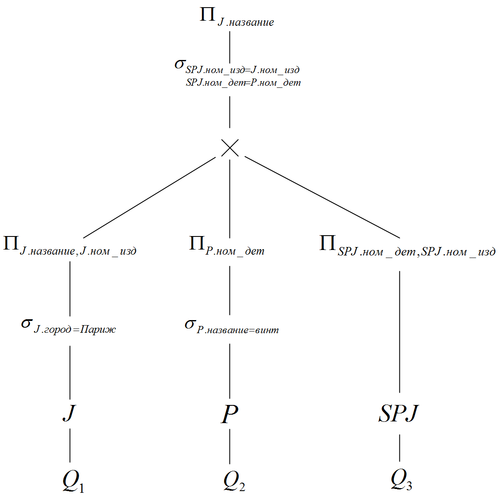
Генерация физического плана

1. Необходимо определить, как реализуются подзапросы $$Q_1$$, $$Q_2$$ и $$Q_3$$. Возможно два варианта:
   1. полное сканирование таблицы;
   2. использование индекса;
2. Определить порядок соединения таблиц. Реализуется тремя вложенными циклами;
3. Определить метод соединения.

В результате получится структура $$str[7]$$, в которой будет описано, как лучше соединять.